広島大学 先進理工系科学研究科 情報科学プログラム 2021年8月実施 専門科目I 問題4
Author
祭音Myyura
Description
平面的グラフの次のような自然な一般化を考えよう。グラフ \(G\) は、ユークリッド平面上に各辺が高々 \(1\) 本の他の辺と交差するように描画できるとき \(1\)-平面的 であるという。 ただし任意の \(3\) 辺が \(1\) 点で交差することは許されないものとする。
(1) \(1\)-平面的ではあるけれども平面的ではないグラフの例を示しなさい。ただし、そのグラフが平面的でないことの理由も示すこと。
(2) 定義より、任意の平面的グラフは1-平面的でもある。頂点数6以下の任意のグラフが1-平面的であることを証明しなさい。
(3) 任意の1-平面的グラフの点彩色数は高々で6であることが知られている。 (1) で答えたグラフを色集合 \({a, b, c, d, e, f}\) を使って点彩色しなさい。 ただし隣接する任意の2頂点が異なる色で塗られていなくてはならないものとする。
Let us consider the following natural generalization of planar graphs. A graph is said to be 1-planar if it can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point with other edge and any three edges do not cross at a point.
(1) Give an example of a 1-planar graph which is not planar, with a certification of non-planarity.
(2) By definition, any planar graph is 1-planar. Prove that any graph with at most six vertices is 1-planar.
(3) It is known that the chromatic number of any 1-planar graph is at most six. Give a vertex coloring of the graph illustrated in (1) with a set of colors \({a, b, c, d, e, f}\) in such a way that any two adjacent vertices are given different colors.
Kai
(1)
The graph \(K_5\) (complete graph of \(5\) vertices) is not planar but 1-planar (Fig 1.)
Fig 1.
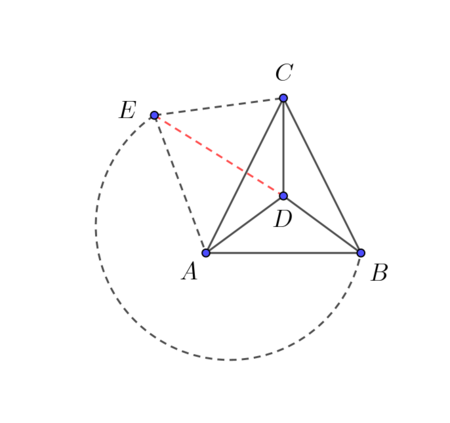
To show \(K_5\) is not planar, first we note that the complete graph \(K_4\) is planar (see Fig 1., vertices \(A, B, C, D\)).
Now we attempt to create \(K_5\) by building it from it subgraph \(K_4\). Each of the faces of \(K_4\) is in the same form as each of the others. That is, each face consists of a triangle of 3 vertices which is not incident to the 4th vertex. So exactly where in the plane we place the 5th vertex does not matter.
W.l.o.g let us place vertex \(E\) outside the triangle \(ABC\) as shown above. Edges \(AE\), \(BE\), and \(CE\) can be constructed without crossing an existing edge of \(K_4\), as indicated by dotted black lines, then it is not possible to construct edge \(DE\) without crossing one of \(AB\), \(AC\) or \(BC\). This is shown in dotted red. Hence \(K_5\) is not planar.
(2)
To prove that any graph with at most six vertices is 1-planar, we only need to prove that \(K_6\) is 1-planar since any graph with at most six vertices is a subgraph of \(K_6\).
We place another vertex \(F\) in the outerface of Fig.1. Edge \(AF\) can be constructed by crossing \(BE\), edge \(DF\) can be constructed by crossing \(BC\) and edges \(BF\), \(CF\), \(EF\) can be constructed without crossing an existing edge. Hence the result.
(3)
(意味不明な設問)
- A: a
- B: b
- C: c
- D: d
- E: e