広島大学 先進理工系科学研究科 情報科学プログラム 2020年8月実施 専門科目I 問題4
Author
samparker, 祭音Myyura
Description
任意の 2 辺を辺の端点以外で交差させることなく平面に描画できるようなグラフを平面的であるという。 頂点数 \(v\) 、辺数 \(e\) の連結な平面的グラフ \(G\) を平面描画したときの面の数 \(f\) とすると \(v - e + f = 2\) となることが知られており、この等式はオイラーの公式と呼ばれている(ただし一番外側の領域も一つの面とみなす)。
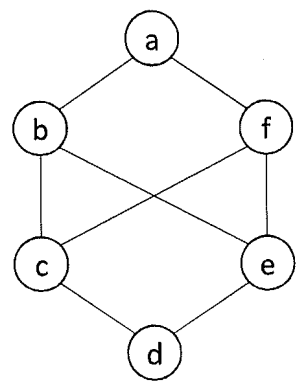
(1) 図 1 に示すグラフ \(G_1\) の平面描画を示し、その描画がオイラーの公式を満たしていることを説明せよ。
(2) 単純グラフ \(G = (V, E)\) の補グラフ \(\overline{G}\) は、\(G\) と同じ頂点集合をもち、辺集合 \(\overline{E} = \{(u, v) \in V \times V : (u, v) \notin E\}\) を持つグラフである。グラフ \(G_1\) の補グラフの平面描画を示せ。
(3) 平面性を維持したままでグラフに追加できる辺の数には限界がある。 オイラーの公式を利用して、頂点数 \(v\) 、辺数 \(e\) の単純グラフ \(G\) が平面的であるための必要条件が \(e \leq 3(v - 2)\) となることを示せ。
(4) 不等式 \(e \leq 3(v - 2)\) を利用して、頂点数 \(11\) 以上の任意の単純グラフ \(G\) について、\(G\) か \(\overline{G}\) の少なくとも一方は平面的ではないことを示せ。
A graph is said to be planar if it can be drawn on a plane so that no two edges intersect except at the end vertices of the edges. Let us consider the drawing of a planar graph on a plane. By letting \(f\) be the number of faces (i.e., closed regions including exterior one) in the drawing of a connected planar graph \(G\) with \(v\) vertices and \(e\) edges, it holds \(v - e + f = 2\), which is called the Euler's formula in the graph theory.
(1) Give a planar drawing of graph \(G_1\) shown in Figure 1, and show that the drawing fulfills the Euler's formula.
(2) Complement of simple graph \(G = (V, E)\), denoted as \(\overline{G}\), is a graph with vertex set \(V\) and edge set \(\overline{E} = \{(u, v) \in V \times V : (u, v) \notin E\}\). Give a planar drawing of the complement of graph \(G_1\).
(3) There is an upper limit on the number of edges so that a simple graph is planar. Prove that any simple planar graph with \(v\) vertices and \(e\) edges satisfies \(e \leq 3(v - 2)\).
(4) With inequality \(e \leq 3(v - 2)\), prove that for any simple graph \(G\) with at least 11 vertices, \(G\) or \(\overline{G}\) is not planar.
図1グラフ \(G_1\) Figure 1 Graph \(G_1\)
Kai
(1)
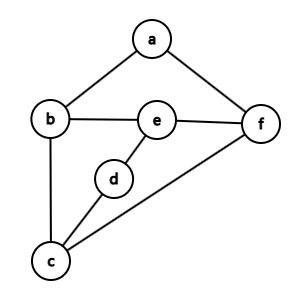
number of vertices: \(v = 6\), number of edges: \(e = 8\), number of faces: \(f = 4\)
(2)
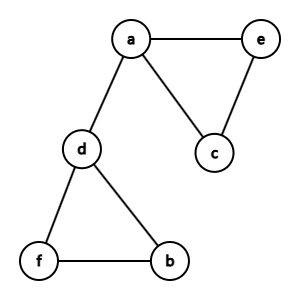
(3)
Suppose a connected graph with \(v\) vertices and \(e\) edges has a planar embedding with \(f\) faces. Since every edge is traversed exactly twice by the face boundaries, the sum of the lengths of the face boundaries is exactly \(2e\). Also, each face boundary is of length at least \(3\), so this sum is at least \(3f\). This implies that
But \(f = e - v + 2\) by Euler’s formula, and substituting into the above gives
(4)
When \(v \geq 11\), w.l.o.g. assume that \(G\) is planar, then by (3) we have
Let \(\bar{e}\) denote the number of edges of \(\overline{G}\). Since the number of edges of \(K_{11}\) (i.e. the complete simple graph of \(11\) nodes) is \(11 \times 10 \div 2 = 55\), we have
Hence \(\overline{G}\) is not planar.