広島大学 先進理工系科学研究科 情報科学プログラム 2020年8月実施 専門科目II 問題2
Author
祭音Myyura
Description
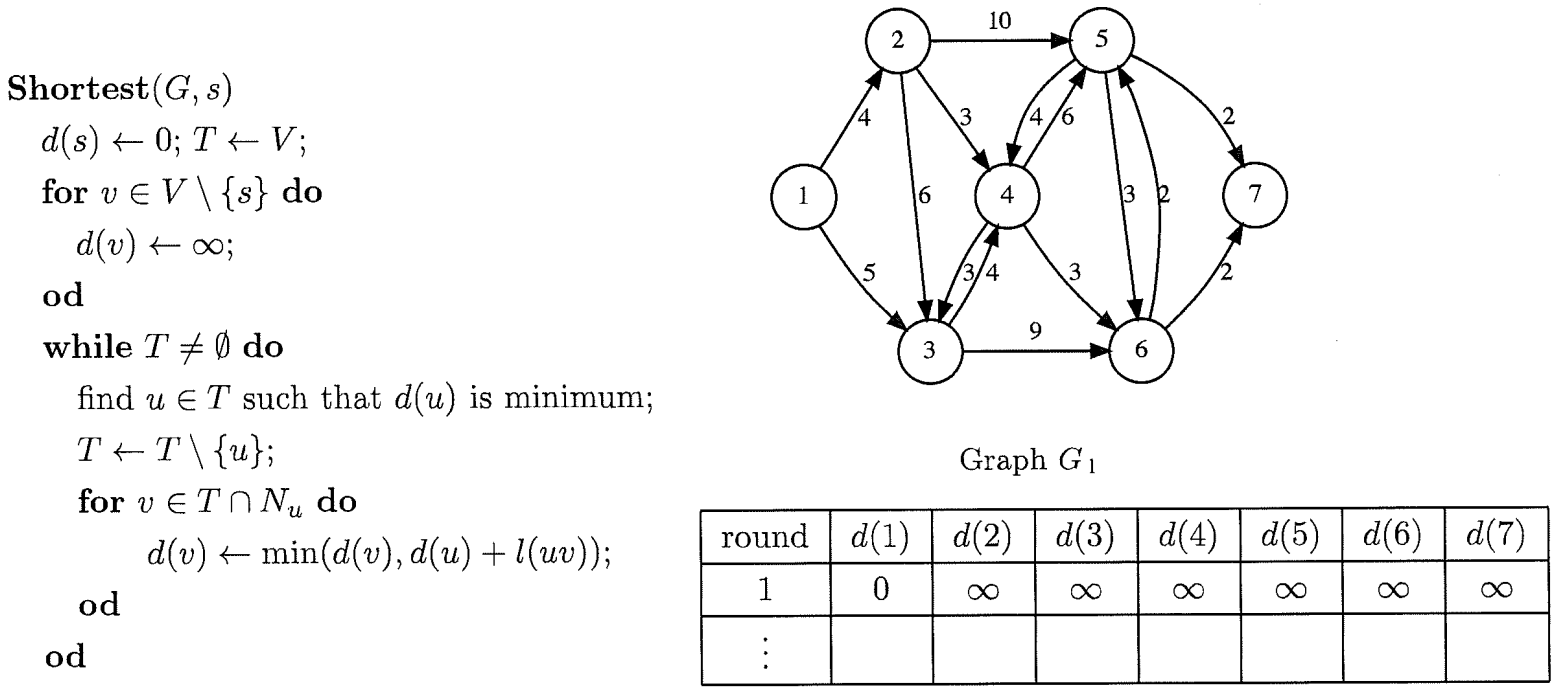
有向グラフ \(G = (V, E, l)\) を考える。 \(V\) は頂点集合、\(E\) は辺集合、\(l(e)\) は辺 \(e\) の長さとする。 また、\(N_v\) を頂点 \(v\) の隣接頂点集合とする。 この時、以下の \(\textbf{Shortest}(G, s)\) は、\(G\) 上のある頂点 \(s\) を始点とし、頂点 \(s\) から他の各頂点までの最短距離を求めるアルゴリズムである。
(1) Table 1 は、グラフ \(G_1\) を入力とし、頂点 \(1\) を始点とした場合の \(\textbf{Shortest}(G_1, 1)\) の実行の過程における、各頂点 \(v\) の \(d(v)\) の値を示したものである。Table 1 を完成させよ。
(2) \(G\) のすべての辺の長さが非負である場合に、\(\textbf{Shortest}(G, s)\) で得られる \(d(v)\) が、すべての頂点 \(v \in V\) について頂点 \(s\) からの最短距離となることを証明せよ。
(3) \(G\) に負の長さの辺が存在する場合には、\(\textbf{Shortest}(G, s)\) は \(s\) からの最短距離を求められない場合があることを証明せよ。
(4) \(\textbf{Shortest}(G, s)\) の最悪計算時間とその理由を述べよ。
Let \(G = (V, E, l)\) be a directed graph, where \(V\) is a set of nodes, \(E\) is a set of edges, and \(l(e)\) is the non-negative length of edge \(e\). Let \(N_v\) be a set of adjacent nodes of node \(v\). The following algorithm \(\textbf{Shortest}(G, s)\) computes the shortest distance from a node \(s\) to each of the other nodes.
(1) Table 1 shows the value of \(d(v)\) for each \(v \in V\) in the process of execution of \(\textbf{Shortest}(G_1, 1)\), where the input graph is \(G_1\) and the starting node is \(1\). Complete Table 1.
(2) Prove that \(d(v)\) for each \(v \in V\) stores the shortest distance from \(s\) to \(v\) when \(\textbf{Shortest}(G, s)\) terminates.
(3) Prove that \(\textbf{Shortest}(G, s)\) may not find the shortest distance if some of the edges take negative length.
(4) Derive the time complexity of \(\textbf{Shortest}(G, s)\).
Kai
(1)
| round | \(d(1)\) | \(d(2)\) | \(d(3)\) | \(d(4)\) | \(d(5)\) | \(d(6)\) | \(d(7)\) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
| 2 | 0 | 4 | 5 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
| 3 | 0 | 4 | 5 | 7 | 14 | \(\infty\) | \(\infty\) |
| 4 | 0 | 4 | 5 | 7 | 14 | 14 | \(\infty\) |
| 5 | 0 | 4 | 5 | 7 | 13 | 10 | \(\infty\) |
| 6 | 0 | 4 | 5 | 7 | 12 | 10 | 12 |
(2)
Proof by contradiction:
Let \(\delta(v)\) denote the length of a shortest path from \(s\) to \(v\). Suppose that \(u\) is the first vertex extracted from \(T\) for which \(d(u) \neq \delta(u)\).
Let \(s \rightarrow P_1 \rightarrow x \rightarrow y \rightarrow P_2 \rightarrow u\) be a shortest path from \(s\) to \(u\), where \(x\) satifies \(d(x) = \delta(x)\) but \(y\) does not. When \(x\) is extracted from \(T\), since \(y\) is adjacent to \(x\), \(d(y)\) will be updated
Now both \(y\) and \(u\) are in \(T\) when \(u\) is chosen. Note that by assumption \(u\) is the first vertex extracted from \(T\) for which \(d(u) \neq \delta(u)\), hence either \(d(y) = \delta(y)\) or \(y\) is chosen after \(u\), which means that \(d(u) \leq d(y)\). But by assumption we have \(d(y) \neq \delta(y)\), hence we have
Thus the two inequalities must be equalities,
a contradiction.
(3)
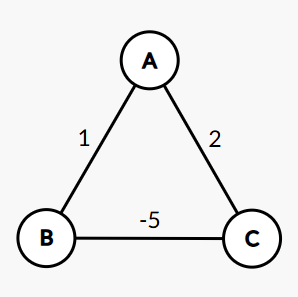
\(\textbf{Shortest}(G, A)\) from \(A\) will first develop \(B\), and will later fail to find \(A \rightarrow C \rightarrow B\).
(4)
If we stores the vertex set \(T\) as a heap, and edges as an adjacent list, then finding \(u\) of minimum \(d(u)\) takes \(O(\log |V|)\).
Note that we need update \(d(v)\) of every \(v \in T \cap N_u\), which can be done by inserting a "new vertex" \(v\) of updated \(d(v)\) into heap \(T\), hence the size of \(T\) is at most \(|E|\).
Therefore, the time complexity of \(\textbf{Shortest}(G, s)\) is \(O(|E|\log |V|)\).