広島大学 先進理工系科学研究科 情報科学プログラム 2019年8月実施 専門科目I 問題4
Author
祭音Myyura
Description
グラフ \(G = (V, E)\) の辺集合 \(A \subseteq E\) は、任意の \(e, e' \in A\) が互いに端点を共有しないときマッチングと呼ばれる。 またそれ以上辺を追加できないマッチングを極大マッチングと呼ぶ。
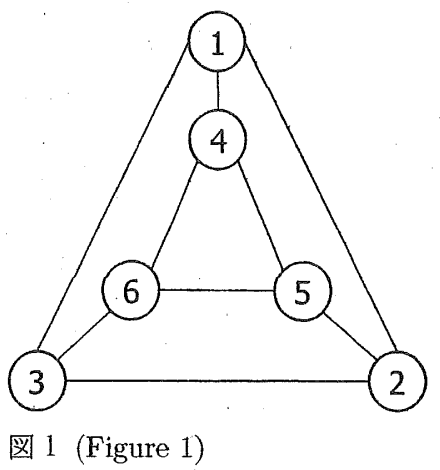
(1) 図 1 に示すグラフの極大マッチングを二つ示せ。
(2) グラフ \(G\) の任意の極大マッチング \(A, B\) に対して \(|A - B| \leq 2|B - A|\) が成立することを証明せよ。 ここで \(A - B = \{ e \in A : e \notin B \}\) であり、\(|A|\) は集合 \(A\) の濃度(cardinality)を表すものとする。
(3) 上の証明と関係 \(|A| = |A \cap B| + |A - B|\) を利用して、\(|A| \leq 2|B|\) であることを証明せよ。
(4) \(|A| = 2|B|\) であるような極大マッチング \(A, B\) を持つグラフの例を示せ。
Given graph \(G = (V, E)\), a subset of edges \(A \subseteq E\) is called a matching if any two edges \(e, e' \in A\) share no end vertex. A matching \(A\) is said to be maximal if any superset of \(A\) is not a matching.
(1) Show two maximal matchings of the graph shown in Figure 1.
(2) Prove \(|A - B| \leq 2|B - A|\) holds for any maximal matchings \(A\) and \(B\) of a given graph \(G\). Here, \(A - B\) is defined as \(A - B = \{ e \in A : e \notin B \}\) and \(|A|\) denotes the cardinality of set \(A\).
(3) Prove \(|A| \leq 2|B|\) by using the above statement and equation \(|A| = |A \cap B| + |A - B|\).
(4) Show an example of graph \(G\) to have maximal matchings \(A\) and \(B\) satisfying \(|A| = 2|B|\).
Kai
(1)
(2)
Note that each edge in \(B - A\) can be adjacent to at most \(2\) edges in \(A - B\) since \(A\) is a matching; and each edge in \(A - B\) is adjacent to an edge in \(B -A\) by maximality of \(B\), hence we have
(3)
(4)
matchings