Skip to content

広島大学 先進理工系科学研究科 情報科学プログラム 2019年8月実施 専門科目II 問題2

Author

samparker, 祭音Myyura

Description

子の数に制約のない根付き木を \(2\) 分木によって表す方法として、左子・右兄弟表現がある。 2 分木の各節点 \(x\) は、キー \(x.key\) の他に、親 \(x.p\) と左端の子 \(x.lc\)、すぐ右の兄弟 \(x.rs\) の３つのポインタを持つ。 親や左端の子、すぐ右の兄弟がいない節点では、それぞれのポインタ \(p, lc, rs\) の値は \(\text{null}\) とする。 例えば、図 1 (a) の根付き木を上述の表現の二分木で表すと図 1 (b) のようになる。

(1) 根付き木の節点の数を \(n\)、枝の数を \(m\) とする。\(m\) と \(n\) の関係を書け。

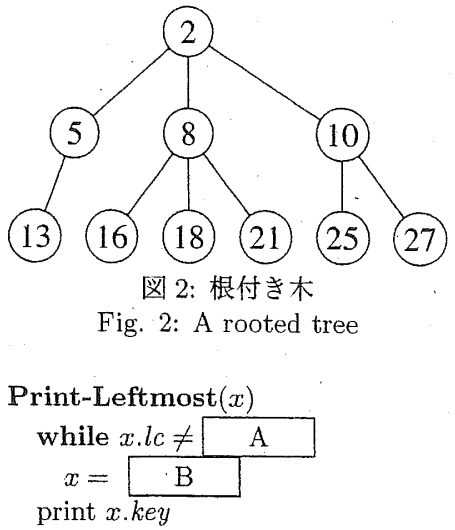
(2) 図 2 の根付き木を、左子・右兄弟表現の 2 分木で表せ。ポインタ \(p\) は省略せよ。

(3) 根付き木の根 \(x\) が与えられたとき、一番左下の子孫の \(key\) を出力する手続きの擬似コード Print-Leftmost(\(x\)) を示す。空欄 \(\boxed{\ A \ }\) と \(\boxed{\ B \ }\) を適切に埋めよ。

(4) 根付き木の根 \(x\) が与えられたとき、すべての節点の \(key\) を出力する手続き Tree-Walk(\(x\)) を擬似コードで書け。ただし、節点を出力する順序は問わない。

(5) (4) の手続き Tree-Walk(\(x\)) の時間計算量をオーダー表記で書け。

There is the left-child, right-sibling representation that uses a binary tree to represent a rooted tree with arbitrary number of children. Each vertex \(x\) of the binary tree contains a key \(x.key\), a parent pointer \(x.p\), a pointer to the leftmost child \(x.lc\), and a pointer to the sibling immediately to its right \(x.rs\). We assume that, in case of no parent, no child, or no sibling, the value of the pointer \(p, lc,\) or \(rs\) is null, respectively. For example, a rooted tree shown in Fig. 1 (a) is represented by a binary tree of the above representation as shown in Fig. 1 (b).

(1) We assume that a rooted tree has \(n\) vertices and \(m\) edges. Describe the relationship between \(m\) and \(n\).

(2) Draw a binary tree of the left-child, right-sibling representation, to represent a rooted tree shown in Fig. 2. The pointer \(p\) should not be drawn.

(3) The pseudo code Print-Leftmost(\(x\)) is a procedure that prints the key of the leftmost descendant of a tree rooted at a given node \(x\). Fill the blanks \(\boxed{\ A \ }\) and \(\boxed{\ B \ }\).

(4) Write a pseudo code of the procedure Tree-Walk(\(x\)) that prints keys of all vertices in a tree rooted at a given node \(x\). The order of vertices to print is not the matter.

(5) Show the execution time of Tree-Walk(\(x\)) using big-O notation.

Kai

(1)

\(n = m + 1\)

(2)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
                            2
                        /
                       5
                   /       \
                  13        8
                        /       \
                       16       10
                         \    /
                         18  25
                           \   \
                           21  27

(3)

  • \(\boxed{\ A \ }:\ \text{null}\)
  • \(\boxed{\ B \ }: \ x.lc\)

(4)

1
2
3
4
5
Tree-Walk(x)
    if (x != null) then
        print(x.key)
        Tree-Walk(x.lc)
        Tree-Walk(x.rs)

(5)

\(O(n)\)