東京工業大学 工学院 電気電子系 2018年度 電磁気学 2
Author
Zero, 祭音Myyura
Description
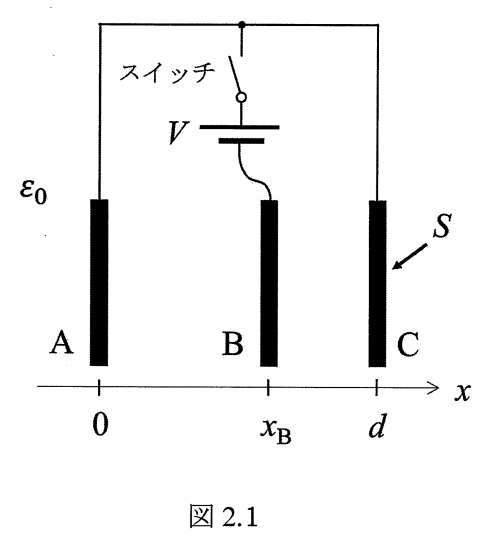
図2.1のように、誘電率 \(\varepsilon_0\) の真空中に面積 \(S\) の同じ形状の平板電極 \(A、B、C\) を \(x\) 軸上に沿って平行に置く。
電極 \(A\) と \(C\) はそれぞれ \(x = 0\) 、\(x = d\) で固定されており、電極 \(B\) は外力によって \(x\) 軸に沿って移動させることができるものとする。
電極 \(B\) の位置を \(x = x_B\) として、以下の間に答えよ。ただし、平板電極の厚さと端部効果は無視するものとする。
すべての電極で初電荷 0 の状態から電極 \(A\) と \(C\) を導線で接続し、スイッチを閉じて導線と電極 \(B\) の間に電位差 \(V\) を印加した。
(1) 電極 \(A\) と電極 \(C\) それぞれに蓄えられる電荷量 \(Q_A\) 、\(Q_C\) を求めよ。
(2) この系が蓄えている静電エネルギーを求めよ。
(3) 電極 \(B\) にはたらく静電力の大きさと向きを求めよ。
(4) \(x_B = d/2\) の状態でスイッチを開き、電極 \(B\) に電荷が蓄えられたままとする。この状態から電極 \(B\) を移動させ \(x_B > d/2\) としたとき、この系が蓄えている静電エネルギーを求めよ。
(5) このとき、電極 \(A\) と電極 \(C\) それぞれに蓄えられる電荷量 \(Q'_A\)、\(Q'_C\) を求めよ。
(6) 電極 \(B\) を一定の速度 \(v\) で \(x\) 軸の正方向に移動させると、\(AC\) を結ぶ導線に電流が流れた。この電流 \(I\) の大きさと向きを求めよ。
Kai
(1)
\[
\begin{aligned}
&E_A = \frac{Q_A}{\varepsilon_0 S} \\
&V = x_BE_A = \frac{Q_A}{\varepsilon_0 S}x_B \\
&\quad \Rightarrow Q_A = \frac{\varepsilon_0 S}{x_B}V \\
&E_C = \frac{Q_C}{\varepsilon_0 S} \\
&V = (d - x_B)E_C = \frac{Q_C}{\varepsilon_0 S}(d - x_B) \\
&\quad \Rightarrow Q_C = \frac{\varepsilon_0 S}{d - x_B}V
\end{aligned}
\]
(2)
\[
\begin{aligned}
U &= \frac{1}{2}Q_AV + \frac{1}{2}Q_CV \\
&= \frac{1}{2}\frac{\varepsilon_0 S}{x_B}V^2 + \frac{1}{2}\frac{\varepsilon_0 S}{d - x_B}V^2 \\
&= \frac{1}{2}\varepsilon_0 S V^2\bigg(\frac{1}{x_B} + \frac{1}{d - x_B}\bigg)
\end{aligned}
\]
(3)
\[
\begin{aligned}
F = \frac{\partial U}{\partial x_B} &= \frac{1}{2}\varepsilon_0 SV^2\bigg(-\frac{1}{x_{B}^2} + \frac{1}{(d - x_B)^2}\bigg) \\
&= \frac{1}{2}\varepsilon_0 SV^2 \bigg(\frac{-d^2 + 2x_Bd - x_B^2 + x_B^2}{x_B^2(d - x_B)^2}\bigg) \\
&= \frac{1}{2}\varepsilon_0 SV^2 \bigg(\frac{(2x_B - d)d}{x_B^2(d - x_B)^2}\bigg) \\
&= \varepsilon_0 SV^2 \frac{(x_B - \frac{d}{2})d}{x_B^2(d - x_B)^2}
\end{aligned}
\]
\(\frac{d}{2} > x_B\) で, \(x\) 軸負方向
\(\frac{d}{2} < x_B\) で, \(x\) 軸正方向
\(x_B = \frac{d}{2}\)で, \(F = 0\)
(4)
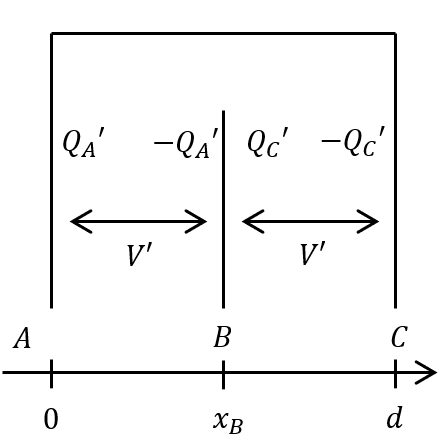
電荷保存則より,
\[
\begin{aligned}
Q = Q_A + Q_C &= \frac{2\varepsilon_0 S}{d}V + \frac{2\varepsilon_0 S}{d}V \\
&= \frac{4\varepsilon_0 S}{d}V \\
Q = Q_A' + Q_C' &= Q_A + Q_C \\
C_A' &= \frac{\varepsilon_0 S}{x_B} \\
C_C' &= \frac{\varepsilon_0 S}{d - x_B}
\end{aligned}
\]
スイッチを開いた後のそれぞれの電極間の電位差を \(V'\) とすると,
\[
\begin{aligned}
Q &= Q_A' + Q_C' \\
&= \frac{\varepsilon_0 S}{x_B}V' + \frac{\varepsilon_0 S}{d - x_B}V' \\
&= \varepsilon_0 S V' \bigg(\frac{1}{x_B} + \frac{1}{d - x_B}\bigg) \\
&= \frac{4\varepsilon_0 S}{d}V \\
\Rightarrow \\
V' &= \frac{4V}{d(\frac{1}{x_B} + \frac{1}{d - x_B})} \\
&= \frac{4x_B(d - x_B)}{d(d - x_B + x_B)}V \\
&= \frac{4x_B(d - x_B)}{d^2}V
\end{aligned}
\]
よって, 静電エネルギーは
\[
\begin{aligned}
&\frac{1}{2}(C_A' + C_C')(V')^2 \\
&= \frac{1}{2}\varepsilon_0 S(\frac{1}{x_B} + \frac{1}{d - x_B})(\frac{4x_B(d - x_B)}{d^2}V)^2 \\
&= \frac{1}{2}\varepsilon_0 S \frac{d}{x_B(d - x_B)} \cdot \frac{16[x_B(d - x_B)]^2}{d^4}V^2 \\
&= 8\varepsilon_0 S \frac{x_B(d - x_B)}{d^3}V^2
\end{aligned}
\]
(5)
\[
\begin{aligned}
Q_A' &= C_A'V' \\
&= \frac{\varepsilon_0 S}{x_B} \cdot \frac{4V}{d(\frac{1}{x_B} + \frac{1}{d - x_B})} \\
&= \frac{4\varepsilon_0 S V x_B(d - x_B)}{x_B d^2} \\
&= \frac{4\varepsilon_0 S(d - x_B)}{d^2}V \\
Q_C' &= C_C'V' \\
&= \frac{\varepsilon_0 S}{d - x_B} \cdot \frac{4Vx_B(d - x_B)}{d^2} \\
&= 4\varepsilon_0 S \frac{x_B}{d^2}V
\end{aligned}
\]
(6)
\(x_B > \frac{d}{2}\) より,
\[
\begin{aligned}
I &= |-\frac{\text{d}Q_A'}{\text{d}t}| = |\frac{\text{d}Q_C'}{\text{d}t}| \\
&= \frac{4\varepsilon_0 S}{d^2}V \frac{\text{d}x_B}{\text{d}t} \\
&= \frac{4\varepsilon_0 S v}{d^2} V
\end{aligned}
\]
\(A\) から \(C\) に向かう向き

