東京工業大学 工学院 電気電子系 2018年度 電磁気学 1
Author
Zero, 祭音Myyura
Description
真空中の静磁場に関する以下の問に答えなさい。真空中の透磁率を \(\mu_0\) とする。
\(z\) 軸上を負から正の方向に単位長さ当たり \(n\) 個の粒子が速度 \(v\) で等速運動している。速度 \(v\) は光速に比べて十分小さい。粒子は正の電荷 \(q\) をもち、\(n\) が十分大きい場合を考える。
(1) 位置 \(A(x, y, 0)\) における磁束密度ベクトル \(\mathbf{B}_A\) の大きさ \(B_A\) を求めなさい。
(2) 磁束密度ベクトル \(\mathbf{B}_A\) の単位ベクトル \(\hat{\mathbf{B}}_A\) を求めなさい。
(3) 原点から \(a\) 離れた位置に \(z\) 軸に平行に、太さの無視できる無限の長さの導線が置かれており、\(z\) 座標の負から正の方向に電流 \(i\) が流れている。この導線の単位長さあたりに働く力 \(\mathbf{F}\) の大きさと向きを答えなさい。
次に、半径 \(a\) の軌道上を正の電荷 \(q\) を持つ粒子が等速円運動をしている場合を考える。粒子は光速に比べて十分小さい速度 \(u\) で運動している。また、粒子の数は単位長さあたり \(n\) であり、\(n\) が十分大きい場合を考える。
(4) 軌道上を流れる電流の大きさ \(I\) を答えなさい。
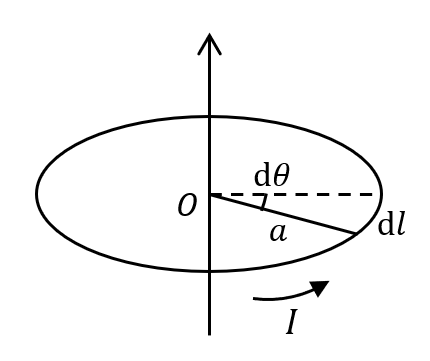
(5) 円軌道の中心 \(O\) における磁束密度の大きさ \(B_0\) を答えなさい。
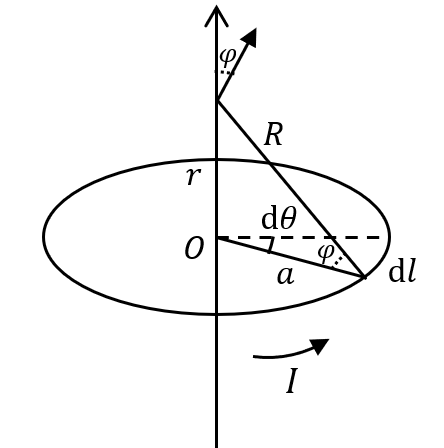
(6) 円軌道の中心 \(O\) を通り円軌道を含む平面に垂直な軸を円軌道の中心軸とよぶ。円軌道の中心軸上の点 \(P\) における磁束密度の大きさ \(B_P\) を答えなさい。ただし、\(OP = r\) とする。
Kai
(1)
アンペールの法則より、
\[
\begin{aligned}
2\pi r \cdot B_A &= \mu_{0}qnv \\
B_A &= \frac{\mu_{0}qnv}{2\pi r} \\
&= \frac{\mu_{0}qnv}{2\pi \sqrt{x^2 + y^2}}
\end{aligned}
\]
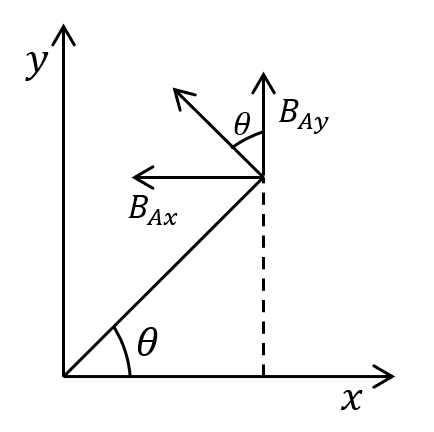
(2)
\[
\begin{aligned}
&B_A = B_{Ax}\hat{x} + B_{Ay}\hat{y} \\
&B_{Ax} = -B_A\sin\theta \\
&B_{Ay} = B_A\cos\theta \quad \text{より、} \\
&(\cos\theta = \frac{x}{\sqrt{x^2 + y^2}},\sin\theta = \frac{y}{\sqrt{x^2 + y^2}}) \\
& \mathbf{B}_A = B_A(\frac{-y}{\sqrt{x^2 + y^2}}\hat{x} + \frac{x}{\sqrt{x^2 + y^2}}\hat{y}) \\
&\therefore \hat{\mathbf{B}}_A = \frac{\mathbf{B}_A}{B_A} = -\frac{y}{\sqrt{x^2 + y^2}}\hat{x} + \frac{x}{\sqrt{x^2 + y^2}}\hat{y}
\end{aligned}
\]
(3)
\[
\begin{aligned}
B_a &= \frac{\mu_0 qnv}{2\pi a} \\
F &= IB_a \cdot 1 \\
&= \frac{\mu_0 qnv}{2\pi a} I
\end{aligned}
\]
引き合う方向
(4)
\[
I = qn v
\]
(5)
ビオ・サバールの法則より、
\[
\begin{aligned}
\text{d}B_0 &= \frac{\mu_0 I}{4\pi a^2}\text{d}l \\
&= \frac{\mu_0 I}{4\pi a^2}a \text{d}\theta \\
B_0 &= \frac{\mu_0 I}{4\pi a}\int_{0}^{2\pi}\text{d}\theta \\
&= \frac{\mu_0 I}{4\pi a} \cdot 2\pi = \frac{\mu_0 I}{2a} \\
&\therefore B_0 = \frac{\mu_0 qn v}{2a}
\end{aligned}
\]
(6)
ビオ・サバールの法則より、
\[
\begin{aligned}
\text{d}B_P &= \frac{\mu_0 I \text{d} l}{4\pi R^2} \cdot \frac{a}{R} \\
&= \frac{\mu_0 I}{4\pi R^2}a\text{d}\theta \cdot \frac{a}{R} \\
&= \frac{\mu_0 I}{4\pi R^3}a^2 \text{d}\theta
\end{aligned}
\]
\[
\begin{aligned}
B_P &= \frac{\mu_0 I a^2}{4\pi(a^2 + r^2)^{\frac{3}{2}}}\int_{0}^{2\pi}\text{d}\theta \\
&= \frac{\mu_0 I a^2}{4\pi(a^2 + r^2)^{\frac{3}{2}}} \cdot 2\pi \\
&= \frac{\mu_0 qn v a^2}{2(a^2 + r^2)^{\frac{3}{2}}}
\end{aligned}
\]