東京工業大学 情報理工学院 数理・計算科学系 2018年度 午前 問C
Author
祭音Myyura
Description
以下の図に示すような \(n \times m\) の格子を考える.ただし \(n \geq m \geq 1\) とする.
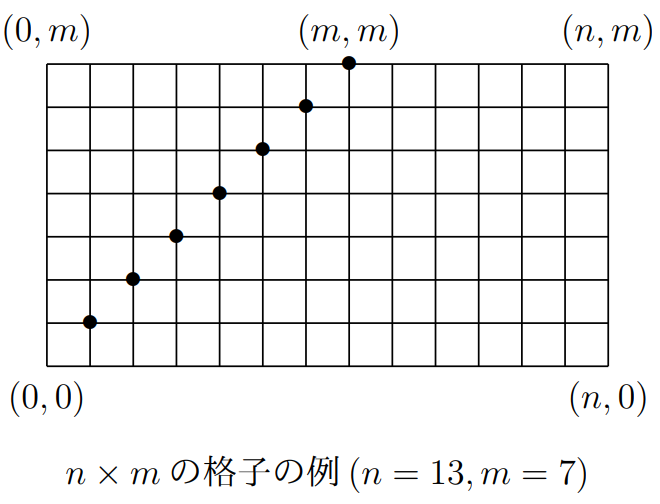
ここで,点 \((0, 0)\) から点 \((n, m)\) まで,条件 1 を満たすように隣接する点の間を移動する経路全体の集合を \(\mathcal{P}(n, m)\) とする.
- 条件 1: 経路上の全ての点に関して,その右または上の隣接点へのみ移動可能.
有限集合 A に対して |A| は A の濃度 (要素数) を表すものとする.
(1) \(|\mathcal{P}(n,m)|\) を求めよ.
\(\mathcal{P}(n,m)\) に含まれる経路で,条件 2 を満たす経路全体の集合を \(\mathcal{B}(n, m) \subseteq \mathcal{P}(n, m)\) とする.
- 条件 2: ある \(a \in \{1, . . . , m\}\) に対して,経路上に点 \((a, a)\) が存在する.すなわち,経路は上図に示した • 印の点を少なくとも 1 つ経由する.
集合 \(\mathcal{B}(n,m)\) を \(\mathcal{B}_{(0,1)}(n,m) \subseteq \mathcal{B}(n,m)\) と \(\mathcal{B}_{(1,0)} \subseteq \mathcal{B}(n,m)\) に分割する.
- \(\mathcal{B}_{(0,1)}(n,m): \mathcal{B}(n,m)\) に含まれる経路で,点 \((0, 1)\) を通る経路全体の集合.
- \(\mathcal{B}_{(1,0)}(n,m): \mathcal{B}(n,m)\) に含まれる経路で,点 \((1, 0)\) を通る経路全体の集合.
(2) \(|\mathcal{B}_{(0,1)}(n,m)|\) を求めよ.
(3) \(|\mathcal{B}_{(1,0)}(n,m)|\) を求めよ.
(4) \(r(n,m) = \frac{|\mathcal{G}(n,m)|}{|\mathcal{P}(n,m)|}\) | を求めよ.ただし \(\mathcal{G}(n,m) = \mathcal{P}(n,m) \setminus \mathcal{B}(n,m)\). また \(n = 15, m = 10\) として \(r(15, 10)\) を求めよ.
Kai
(1)
Total number of moves in which we have to move up to reach the last row \(= m\)
Total number of moves in which we have to move right to reach the last column \(= n\)
Total moves \(= m + n\)
Now think of moves as a string of ‘R’ and ‘U’ characters where ‘R’ at any ith index will tell us to move ‘Right’ and ‘U’ will tell us to move ‘Up’. Then \(\mathcal{P}(n,m)\) equals to how many unique strings (moves) we can make where in total there should be \((n + m)\) characters and there should be \(m\) ‘U’ character and \(n\) ‘R’ character. Note that choosing positions of \(n\) ‘R’ characters results in the automatic choosing of \(m\) ‘U’ character positions
Therefore,
(2)
Note that all paths go through the point \((0,1)\) will cross the line \(y=x\), hence
(3)
We take a path from \((1,0)\) to \((n,m)\) which touch (cross) the line \(y=x\), and let \(p\) be the point where it first touches this line.
If we reflect the portion of the path from \((1,0)\) to \(p\) around the line \(y=x\), then we get a path from \((0,1)\) to \((n,m)\). Conversely, any path from \((0,1)\) to \((n,m)\) must cross the line \(y=x\). If we let \(p'\) be the point where the path first touches this line and reflect the portion of the path from \((0,1)\) to \(p'\) about this line, then we get a path from \((1,0)\) to \((n,m)\).
Since this gives a bijection between the two types of paths, and since the number of paths from \((0,1)\) to \((n,m)\) is given by \(\mathcal{B}_{(0,1)} (n,m)\), we have
(4)
By (2) and (3) we have
Then