Skip to content

東京工業大学 情報理工学院 情報工学系 2017年度 午前 3.

Author

祭音Myyura

Description

部分和問題を解くプログラムを考える。 部分和問題とは、\(n\) 個 \((n \le 1)\) の非負整数の集合 \(A = \{a_0, \ldots, a_{n-1}\}\) と非負整数 \(k\) が与えられたときに、\(A\) の中から \(0\) 個以上の要素を選び、その和が \(k\) に等しくできるときに \(1\)、どう選んでも等しく出来ないときに \(0\) を返す問題である。 すなわち \((\sum_{a \in S} a = k\) である \(A\) の部分集合 \(S\ (S \subseteq A)\) が存在するときに \(1\)、そうでないときに \(0\) を返す。

この問題を解くためのＣ言語プログラムに関して、問 1), 2) および 3) に答えよ。 なお、非負整数の集合 \(A\) の要素は int 型の配列変数 a[] で与えられるものとし、配列のサイズは十分大きいとする。 a[], int 型の変数 k, n は大域変数として宣言されているものとする。 また問題中に出現する int 型の配列変数 b[][] も大域変数として宣言され、そのサイズも十分大きいとする。 空欄 ([ ① ] など) には、1つの式が入るものとする。

なおＣ言語では、真偽値 (true, false) は、int 型の値で表し、if 文などで使用される条件式の実行結果が、真のときはその条件式は \(1\)、偽のときはその条件式は \(0\) を返す。 例えば、比較演算子 == を使った条件式 3==3 は \(1\) を返す。

1). 図 3.1 のように部分和問題を解く 2 引数の関数 f を再帰呼び出しを使って定義した。この関数 f に関して以下の問いに答えよ。

1
2
3
4
int f(int s, int i) {
    if (i == n) { return s == k; }
    else { return f(s, i + 1) || f(s + a[i], i + 1); }
}

図 3.1

  • a) a[0]=8, a[1]=2, a[2]=4, n=3, k=7 を与え、f(0, 0) を実行させたとき、その戻り値が何かを答えよ。
  • b) 問 1)-a) と同じ a[0]=8, a[1]=2, a[2]=4, n=3, k=7 を与え、f(0, 0) を実行させたとき、実行が終了するまでの関数 f の呼び出し関係を樹形図の形式で記述せよ。関数の呼び出し関係の樹形図とは、その関数が呼び出されたときにその関数と渡される引数の値を子ノード、呼び出し元の関数とその引数を親ノードとして、樹形図で書いたものである。例えば、下の樹形図は、関数 h に引数 2, 3 が渡され、実行されると、その実行中に h(1,3) と h(2,2) が呼び出されることを表している。
1
2
3
                            h(2,3)
                          /        \
                      h(1,3)      h(2,2)
  • c) 関数 f の２つの引数 s, i は何を表しているかを説明せよ。

2). 図 3.1 のプログラムの実行時間を改善するために、下記の分を図 3.1 の関数 f の本体の先頭行（プログラムの１行目と２行目の間）に挿入した。この文に関して以下の問いに答えよ。

1
if ([空欄 ①] > k) { return 0; }
  • a) 空欄 [ ① ] を埋めて、文を完成せよ。
  • b) 問 1)-a) と同じ a[0]=8, a[1]=2, a[2]=4, n=3, k=7 を与え、f(0, 0) を実行させたとき、実行が終了するまでの関数 f の呼び出し関係を樹形図の形式で記述せよ。
  • c) 図 3.1 のプログラムと比べて、何が改善されたかを理由とともに述べよ。

3). 再帰呼び出しを使用せずに、部分和問題を解くプログラムを作ることを考える。 \(n \ge 2\)、集合 \(A=\{a_0, \ldots, a_{n-2}, a_{n-1}\}\) において \(A'=\{a_0, \ldots, a_{n-2}\}\) とすると、以下の性質 3.1 が成り立つことに気づいた。

  • \(\sum_{a \in T} a = k\) となる \(A\) の部分集合 \(T\ (T \subseteq A)\) が存在することの必要かつ十分な条件は、\(\sum_{a \in U} a = k\) である \(A'\) の部分集合 \(U\ (U \subseteq A')\) が存在するか、または \(\sum_{a \in V} a = k -\) [空欄 ②] である \(A'\) の部分集合 \(V\ (V \subseteq A')\) が存在するかである。

性質 3.1 を使って、配列変数 b[][] を導入し、図 3.2 のような関数 g のプログラムを作成した。 性質 3.1 と図 3.2 について、以下の問いに答えよ。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
int g(void) {
    int i, j;
    b[0][0] = 1;
    for (i = 0; i < n; i++) {
        for (j = 1; j <= k; j++) { b[i][j] = 0; }
        for (j = 0; j <= k; j++) {
            if (空欄 [③]) { b[i][j] = 1; }
            if (i > 0) {
                if (b[i-1][空欄 [④]]) { b[i][j] = 1; }
                if (j >= a[i]) {
                    if (b[i-1][空欄 [⑤]]) { b[i][j] = 1; }
                }
            }
        }
    }
    return b[n-1][k];
}

図 3.2

  • a) 性質 3.1 が成り立つように、空欄 [ ② ] を埋めよ。なぜ性質 3.1 が成り立つのかも説明せよ。
  • b) 図 3.2 の３つの空欄 [ ③ ], [ ④ ], [ ⑤ ] を埋めて、関数 g のプログラムを完成させよ。
  • c) a[0]=8, a[1]=2, a[2]=4, n=3, k=6 を与え、g() を実行させたときの戻り値と、配列 b[i][j] (ただし、\(0 \le i \le 2, 0 \le j \le 6\)) に格納されている値を下記のような表形式で示せ。
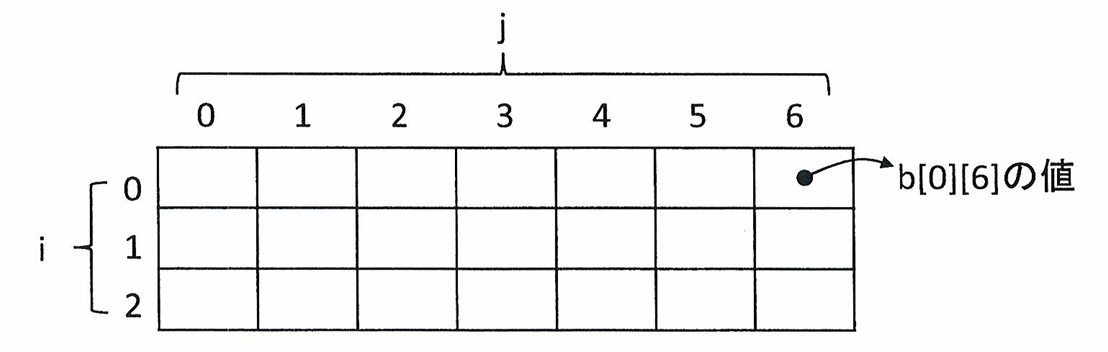
  • d) 配列 b[i][j] の値が \(1\) になったとき、それは何を表しているかを説明せよ。
  • e) 図 3.1 と 図 3.2 のプログラムを比較して、計算時間の観点からどちらが優れているかを論ぜよ。

Kai

1)

a)

0

b)

1
2
3
4
5
6
7
                            f(0,0)
                     /                  \
                  f(0,1)               f(8,1)
              /          \           /        \
            f(0,2)    f(2,2)      f(8,2)       f(10,2)
          /     \     /     \     |     \         |      \
      f(0,3) f(4,3) f(2,3) f(6,3) f(8,3) f(12,3) f(10,3) f(14,3)

c)

引数 i が添字で、i 番目の要素を選ぶか選ばないかを決める。 引数 s は選んでいた要素の総和。

2)

a)

  • 空欄 [ ① ]: s

b)

1
2
3
4
5
6
7
                            f(0,0)
                     /                  \
                  f(0,1)               f(8,1)
              /          \           
            f(0,2)    f(2,2)      
          /     \     /     \     
      f(0,3) f(4,3) f(2,3) f(6,3)

c)

図 3.1 のプログラムと比べて、部分集合の総和が求める値 k を超えた場合の無駄な探索を切り捨てた。

部分集合の総和が求める値 k を超えた場合、残りの要素は正整数なので、これ以上要素を追加しても解を得られない。

3)

a)

  • 空欄 [ ② ]: k - \(a_{n-1}\)

b)

  • 空欄 [ ③ ]: j == 0
  • 空欄 [ ④ ]: j
  • 空欄 [ ⑤ ]: j - a[i]

c)

j=0 j=1 j=2 j=3 j=4 j=5 j=6
i=0 1 0 0 0 0 0 0
i=1 1 0 1 0 0 0 0
i=2 1 0 1 0 1 0 1

d)

図 3.1 のプログラムの計算量は \(O(2^n)\) である。

図 3.2 のプログラムの計算量は \(O(nk)\) である。