東京大学 数理科学研究科 数理科学専攻 2020年8月実施 専門科目 B 第16問

Author

Miyake

Description

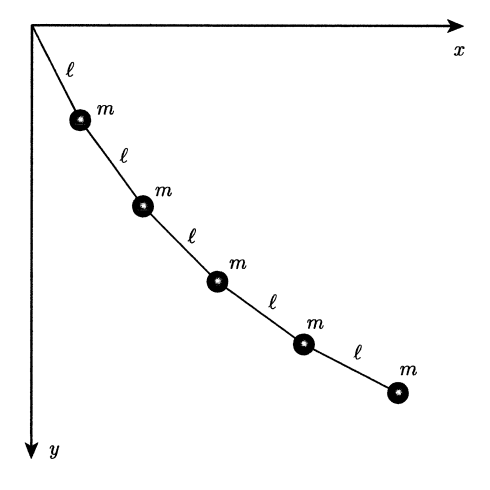
質量が のおもりを 個用意し、図のように長さが の 本のひもで順につないで天井からぶら下げる。 ひもはたわんだり伸び縮みしたりせず、ひもの重さは無視でき、おもりの運動は鉛直軸を含む一定の平面内で起こるものとする。 また、時刻を 、重力加速度を で表すことにする。 図のように、運動が行われる平面の 座標を、天井とひもとの固定点を原点とし、水平方向が 、鉛直下向きを となるように定める。 上から数えて 番目のおもりの水平方向の位置座標を とする。

(1) どの も十分小さいという仮定のもとで、この系のLagrangian 、および から得られる Euler-Lagrange 方程式を求めよ。 ただし、こうして得られる Euler-Lagrange 方程式は、線型の微分方程式になるものとする。

(2) (1)で求めた線型微分方程式の解で、定数 を用いて

と表される解に興味があるとする。 このとき、最高次の係数が のある整数係数 次多項式 が存在し、上の形の解が存在するための必要十分条件が、 と表されることを示せ。

(3) 多項式列 を特徴付ける漸化式を一つ求めよ。

Kai

(1)

位置座標 の時間微分 を それぞれ のように表す。

どの も十分に小さく、 得られる Euler-Lagrange 方程式が線型の微分方程式とのことなので、 運動エネルギーとポテンシャルエネルギーは に関して2次まで求めればよい。

上から数えて 番目のおもりのy座標を とすると、 次が成り立つ：

よって、

なので、この系のポテンシャルエネルギーは（基準点を適当に選んで）

であり、

である。

また、 にくらべて は十分小さいので、 この系の運動エネルギーは

であり、

である。

よって、Langrangian は、

であり、Euler-Lagrange 方程式は、

である。

(2)

(1) で得た運動方程式に を代入して整理すると、次のようになる：

ただし、 は 次の単位行列で、 は 成分が次のように与えられる 次正方行列である：

() が自明な解 以外の解 をもつための必要十分条件は

であるが、これの左辺は に関して 最高次の係数が の整数係数の 次の多項式である。 よって、

として、題意を満たすことがわかる。

(3)

について、

が成り立つ。