東京大学 新領域創成科学研究科 海洋技術環境学専攻 2019年8月実施 第1問~第5問
Author
Description
第1問
次の定積分を求めよ。
第2問
整数
ただし、
この時、以下の問いを答えよ。
1)
2)
第3問
について以下の問いに答えよ。
1)
2)
第4問
座標系
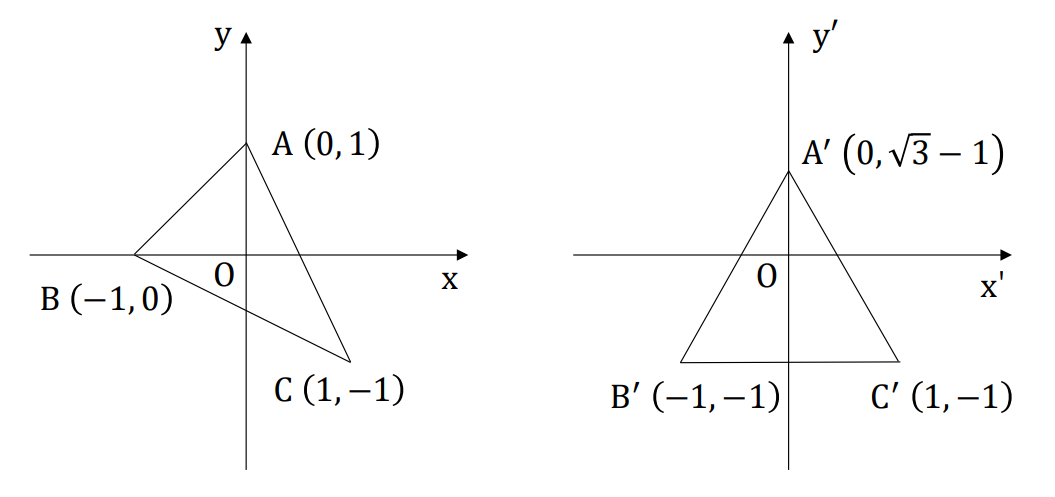
第5問
行列
1) 固有値、固有ベクトルを求めよ。
2)
3)
Kai
第1問
第2問
1)
なので、
2)
であり、これを積分すると、積分定数を
である。
を得る。
第3問
1)
掃き出し法により、次のように求められる:
2)
サラスの方法より、
なので、
第4問
点 A, B, C がそれぞれ 点 A', B', C' に変換されることから、
がわかる。 つまり、
である。
第5問
1)
を得る。
固有値
とおくと
とおくと
である。
2)
1) で求めた固有ベクトルを使って、
とおくと、
が成り立つので、
を得る。
3)
を得る。