東京大学 新領域創成科学研究科 複雑理工学専攻 2019年8月実施 専門基礎科目 第1問

Author

Miyake

Description

以下の間に答えよ。ただし, は実数であるとする。

(間1)

関数 の偏導関数 と を求めよ。また, 曲面 の における接平面の方程式を求めよ。

(間2)

関数 を のまわりで 次の項までテイラー展開せよ。また, 極限

が存在し, を満たすとき, と の値を求めよ.

(間3)

関数 は の 逆関数で, の 定義域と値域は, それぞれ, と であるとする。曲線 を描け。また, この曲線と 軸および 軸で囲まれる領域の面積を求めよ.

(間4)

実関数 が満たす次の微分方程式の一般解を求めよ.

また, 初期値 に対する特解を求めよ。

(間5)

とする。

変数変換 を用いて,次の重積分の値を求めよ。

Kai

（問1）

偏導関数は、

である。

また、 のとき、

であるから、 求める接平面は、点 を通り、法線ベクトル を持つので、 その方程式は、

である。

（問2）

次のように計算できる：

よって、 は1次の項までで次のようにテイラー展開される：

の2次以上の項をまとめて とすると、

であるから、 のときは であり、 のときは発散する。 よって、極限が存在し を満たすのは のときであり、このとき

である。

（問3）

グラフは、このようになります。

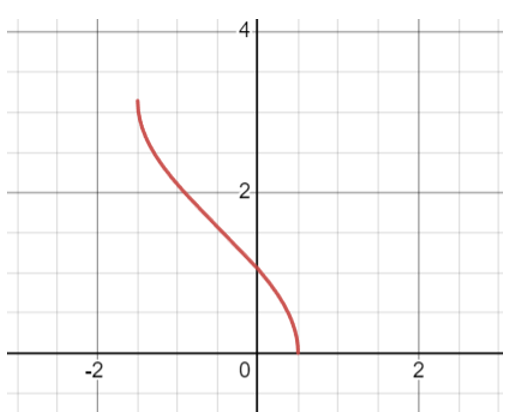
求める面積は、

である。

（問4）

とすると、与えられた微分方程式は、次のように書ける：

そこで、

を考えると、これの一般解は、積分定数を として、

と書ける。 そこで、式 () の解を次のよう形で探す：

これを式 () に代入して整理すると、

よって、

よって、

ここで、 は積分定数である。

また、与えられた初期値を満たすのは、

すなわち、

である。

（問5）

与えられた変数変換について、

であるから、 であり、 与えられた積分は、

となる。