東京大学 工学系研究科 2016年8月実施 数学 第4問

Author

Description

範囲にある実数 , に対して, 3 次元直交座標系 における点 と点 の 2 点を通る直線 を考える。

I.

直線 を,　媒介変数 の一次式として表せ。ただし, の時に点 を,　 の時に点 を表すように定めよ。

II.

を の範囲で変化させたときに直線 が描く曲面 を の方程式として求めよ。また, 曲面 と平面 の交線を とする。 を の方程式として求め, その概形を図示せよ。

次に, 曲面 のガウス曲率を考える。一般に曲面上の点 の位置ベクトル が媒介変数 を用いて,

で与えられるとき,　ガウス曲率 は次式のように表される。

ここで, と は媒介変数 に関する の一階偏微分,　二階偏微分を表している。また, は 3 次元ベクトル の内積, は点 における法線方向の単位ベクトルを表している。

III.

曲面 と 軸の交点のうち領域 にあるものを点 とする。 を満たす に対し,　点 における曲面 のガウス曲率を計算せよ。

IV.

を満たす に対し,　曲面 の任意の点においてガウス曲率が 以下であることを示せ。

Kai

I.

直線 上の点 は,

と表せる。このとき, で , で となり, 題意た満たす。

であるから,　求める直線 の媒介変数表示は,

II.

和積の公式より,

を計算してを消去する。

さらに, を代入して を消去すると,

よって,　求める曲面 の方程式は

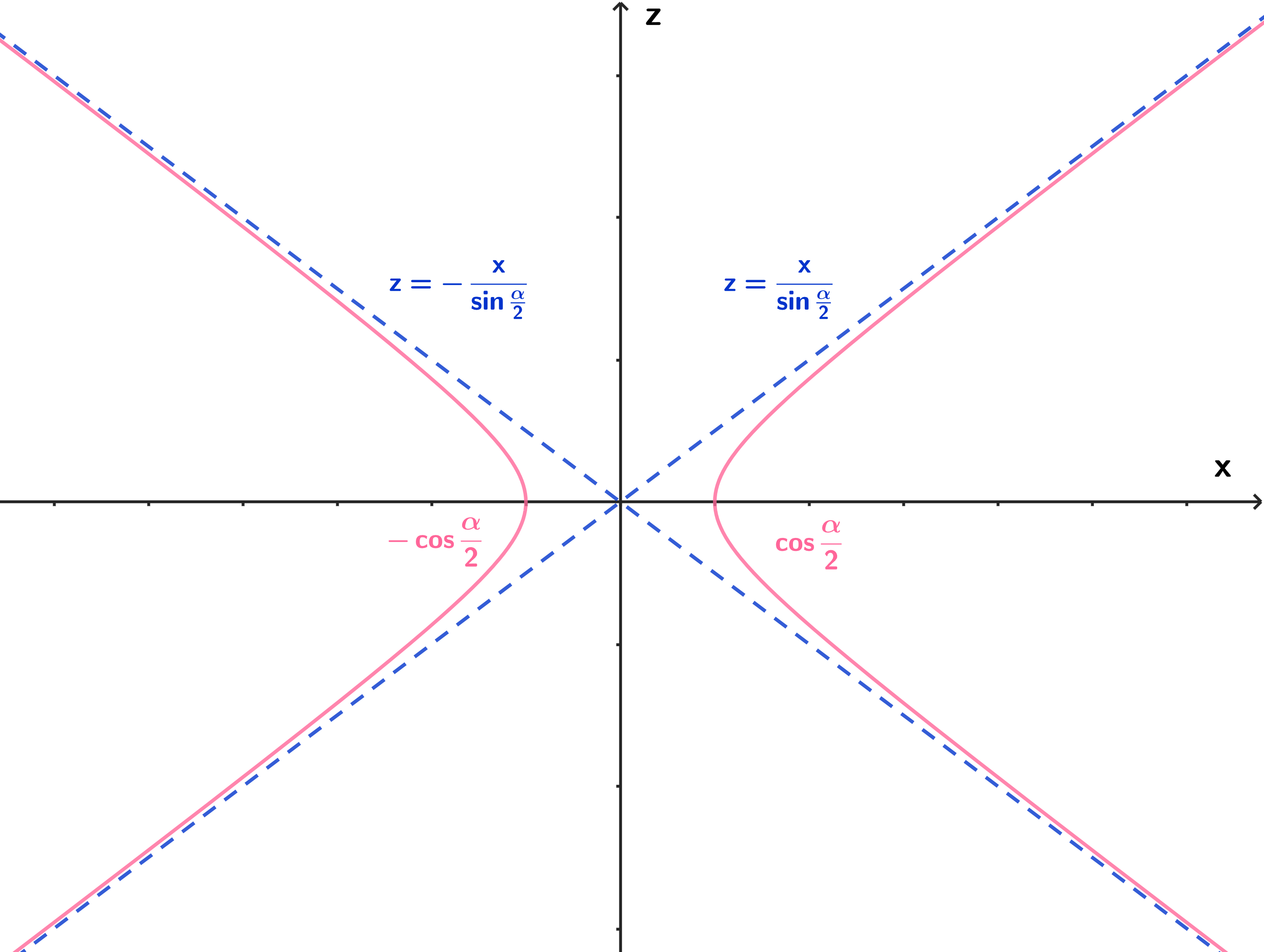
また とすると, 交線 の方程式を得る。

のとき,　 である。

のとき,　この曲線は双曲線であり,　その漸近線の方程式は,　

である。概形は次のようになる。

今,　曲面 上の点 の位置ベクトルは媒介変数 を用いて以下のように表されでおり,

ガウス曲率 は,

で表される。

計算の都合上, 設問 IV から先に解答する。

III.

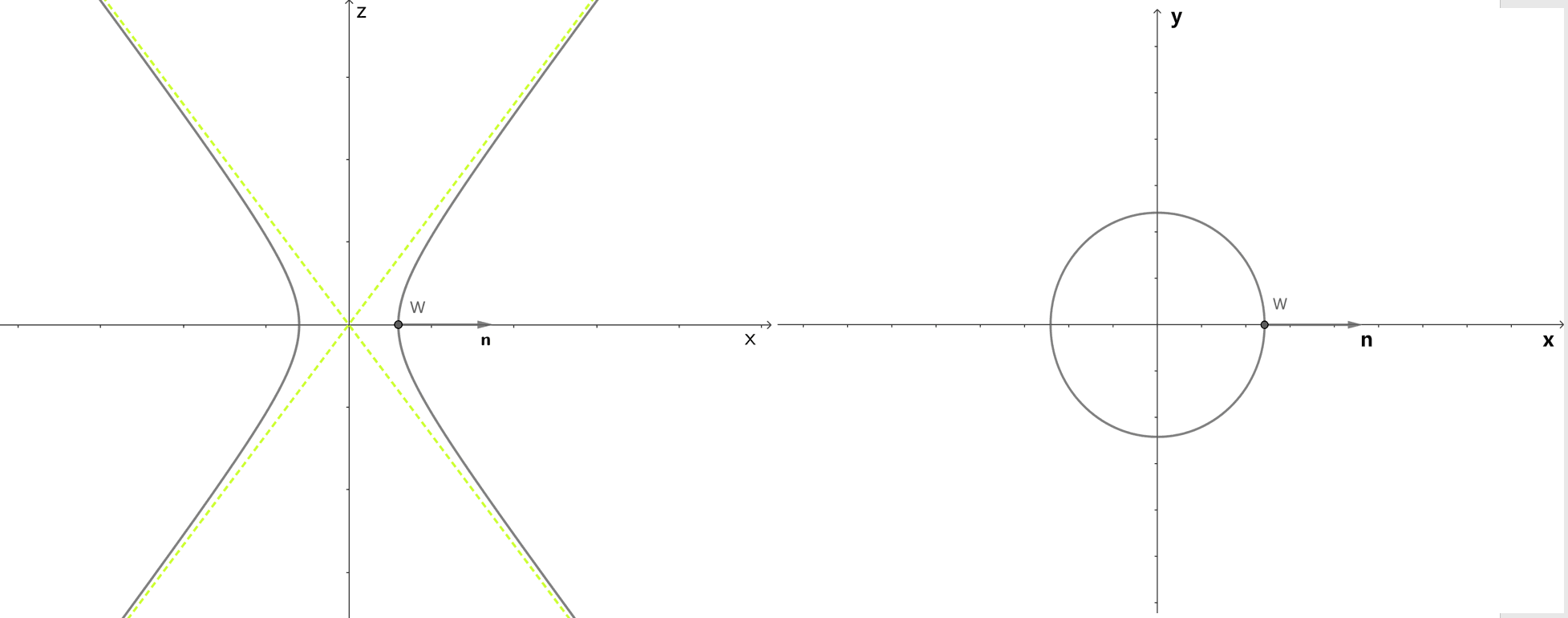
設問 II の図を利用して, 点 における曲面 の法線ベクトル を求める。 平面 での断面が下図左であり, これが双曲線であることから は実数 を用いて の形で表すことができる。

一方で, 平面 で断面は の方程式に を代入することで, 原点を中心とする半径 の円 (下図右) であることが容易に分かる。したがって, は実数 を用いて の形で表すことができる。

これらをともに満たす は, であり, これは単位ベクトルだから点 における単位法線ベクトル は となる。

点 において, は以下の関係を満たす。

3つ目の式より であり, 2つ目の式に代入して,

より,

, より,

の分子は,

の分母は,

したがって求めるガウス曲率 は,

IV.

であることから, の分子は であり, これは明らかに 以下である。従って, の分母が正であることを示せば良い。

であるから, の分母は,

ここで, より, であるから,

である。したがって, が示された。