東京大学 情報理工学研究科 数理情報学 2022年8月実施 第1問

标签：

• Tokyo-University

Author

hari64boli64

Description

正の整数 および有限実数数列 に対して、

と定義する。ただし、 は自然対数を表す。以下の設問に答えよ。

(1) が成り立つことを示せ。また、 となる の必要十分条件を求めよ。

(2) 任意の空でない有限実数数列 に対して、

が成り立つことを示せ。

(3) 任意の実数 に対して、 とおき、 を

で定める。このとき、

となるような関数 の具体的な表式を導出せよ。

(4) が最小となる実数 を求めよ。

Kai

(1)

等号成立条件は、上の式変形より、 である。

(2)

定義に従って示せばよい(変則的だが、分かりやすさの為、左向きの矢印を使用する)。

最後の不等式は、三角不等式より成立する。

以上より、 が示された。

(3)

区分求積法そのままなので、

である。

よって、

となる。

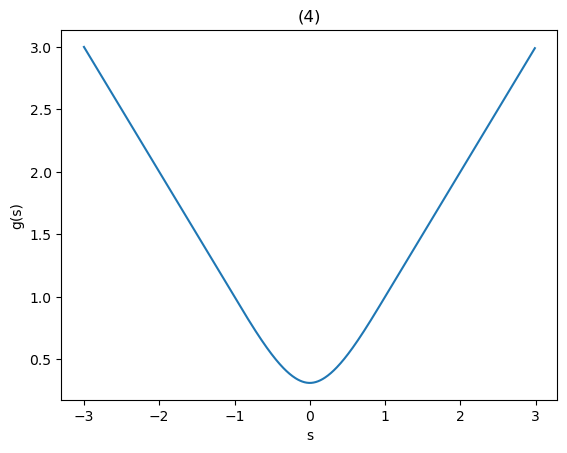
(4)

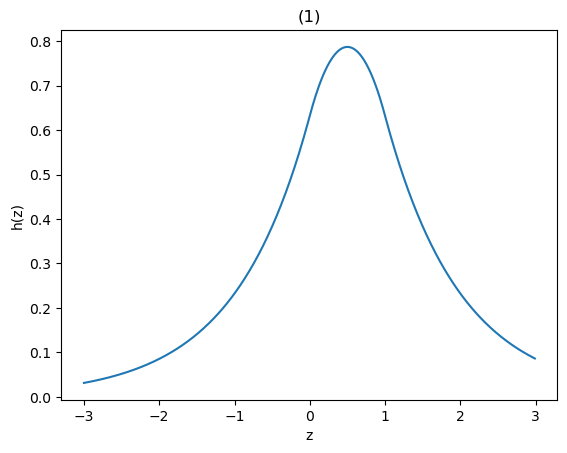
は を中心とする対称関数であり、 微分などを計算すると、図 1 のようになる。

図1: のグラフ

よって、 あまり厳密な議論ではないが、 区間幅1の の最も大きな部分は の時に成立する。 (しかし、これは厳密に行う事も出来るはず)

以上より、 が答え。

実際、これが正しいことは、図 2 より分かる。

図2: のグラフ