東京大学 情報理工学研究科 数理情報学 2019年8月実施 第2問

Author

hari64boli64, Kurosu9991

Description

ある生物の生存時間は平均 の指数分布に従う。 この生物 匹の生存時間を観測することで を推定したい。 ただし実験上の制約により、生まれた直後の一定期間 は観測ができず、もしこの期間内に生物が死んだ場合には、死んだ事実だけが観測されるものとする。 は正の定数である。

に対し、第 番目の個体の生存時間を とおく。 これらは平均 の指数分布に従い、互いに独立とする。 平均 の指数分布の確率密度関数は である。 また観測値 を

と定義する。

以下の問いに答えよ。

(1) の期待値を とおく。 を求めよ。

(2) とおく。 のとき、 を満たす がただ一つ存在することを示せ。

(3) を満たす の個数を とおく。 および に対して

を満たす関数 を求めよ。

(4) かつ のとき、 を最大にする がただ一つ存在することを示せ。

Kai

(1)

の期待値は

(2)

を考える。

存在は、連続性と より明らか。

一意性は、微分すると狭義単調と分かるので明らか。

(3)

まず、 を求める。

より、

次に、 を求める。

ただし、一行目から二行目の変形で、指数分布の無記憶性を用いた。

また、 で、指数分布を 個重ね合わせた分布を示している。

これは、ガンマ分布に従うことが一般に知られている。(後述)

以上より、

(4) - by hari64boli64

に関連する部分だけ取り出すと、

となるが、これを微分するのは大変な困難を伴うように思われる。

なので、別の方針を考える。

ただし、最後の変形で、累積分布関数の微分が確率密度関数になることを用いた。

細かい議論は (2) などと同様になるので省くが、無記憶性を用いた議論や適切な変形を経ると、結局のところ、指数分布の確率密度関数 について、ある値 を取る確率が最大になるような が、ただ一つ存在することを示す問題に帰着されると思われる。 (厳密にはガンマ分布に対して言うべきか?)

これは、(2) の議論とほぼ同様である。

以下では、おまけ程度に、上で示した問題の解を与える。

よって、 となる は、 の時、これのみである。

以上で、大まかには題意が示された。

より詳細な議論を、本来は行うべきであろう。

(4) - by Kurosu9991

に関連する部分だけ取り出すと、

とおくと、

を得る。対数を取って微分すると

を得る。ここで、 は単調減少であり、 , であるから、 は増加から減少に移り変わるので、唯一の極大点を持つことがわかる。

Knowledge

指数分布は再生性を持たない。つまり、 が独立に指数分布に従うとしても、 は指数分布に従わない。 これは一般にはアーラン分布に従う。 特に、今回はガンマ分布に従う。これは以下の畳み込みの式と帰納法で示せる。

同じ指数分布の重ね合わせがガンマ分布になることを示す。

頑張れば、ガンマ分布の形を覚えていなくても、畳み込み計算から示すことが出来る。

指数分布の無記憶性を示す。

---

指数分布の無記憶性とその証明

指数分布とは，「コールセンターに次に電話がかかってくるまでにかかる時間」や「電化製品が次に壊れるまでの時間」などに用いられます。「昨日コールセンターに電話がかかってきたから，今日はかかってこないだろう」とか「昨日電化製品が壊れなかったから，今日は壊れないだろう」とか，そういうことはないわけですから，この事象には，無記憶性があるといえるわけですね。

---

そして、最後の (4) などは、図1が念頭にあると、より分かりやすいと思われる。

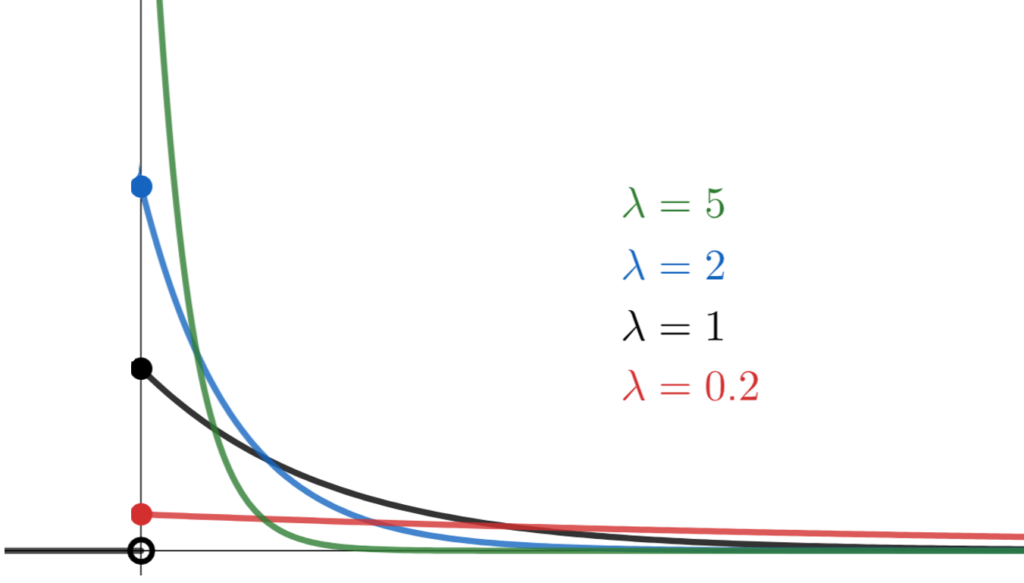
図1 パラメータ毎の指数分布

とある でこのグラフを切った時に、最大の値を取るような は、ただ一つだけというのが、この問題の視覚的な理解であると思われる。