東京大学 情報理工学研究科 2021年8月実施 数学 第3問

Author

Miyake

Description

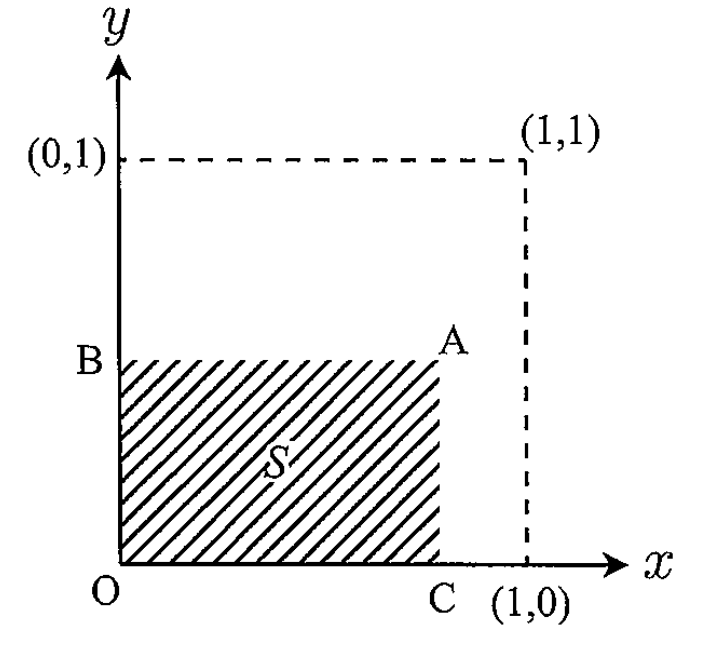
平面上に、かつ で定義される領域 を考える． 上にランダムに1点を選び、それを点 とする．ただし, 点 は 上に一様に分布するとする．図に表すように, 点 から 軸への垂線を ,点 から軸への垂線を とする．原点を としたとき、長方形 を 点 の長方形 と呼ぶ．また、点 の長方形の面積を表す確率変数を とする．以下の問いに答えよ．

(1)、 の期待値を求めよ．

(2)、 となる確率を求めよ．ただし とする．

(3)、 の確率密度関数を求めよ．

再び、領域 を考える． を正の整数とする． 上にランダムに 点を選び,それらを点 とする．ただし、各点は 上に一様に分布し、 である と は独立に選ばれるとする．次の問いに答えよ．

(4)、点 の長方形の面積を表す確率変数を とする． を の最小値を表す確率変数とする．この時、 の確率密度関数を求めよ．

Kai

確率を ，期待値を で表す。

(1)

A の座標を とすると、 は互いに独立な確率変数であり、 それぞれ から までの一様分布に従う。 よって、求める期待値は、

(2)

求める確率は、

(3)

の確率密度関数 は、 では

であり、それ以外では である。

(4)

について

よって、求める確率密度関数 は、

である。 また、 では である。