東京大学 情報理工学研究科 2019年8月実施 数学 第2問

Author

etsurin

Description

平面内の滑らかな曲線 () を考える。 時刻 から までの の長さ は

と定義され、 の全長 を とする。 曲線 は、 とはならないものとする。 時刻 から までの の長さを を変数 で表すと、 を媒介変数 の曲線とみることができる。 そして、 も時刻と呼ぶ。以下の問いに答えよ。

(1) 以下の等式を示せ。

(2) を時刻 における の接線ベクトル と 軸とのなす角とする。 このとき、以下の等式を示せ。

以下では、曲線 は、滑らかな閉曲線で、凸集合 の境界となっているものとする。 また、 は、反時計方向に をまわるものとする。

(3) 任意の時刻 で となることを説明せよ。

(4) に含まれない点 は、時刻 および と の距離 によって、

と一意に表すことができる。 ここで、 は、時刻 における の単位法線ベクトルで、 の外を向いているものとする。 そのような に対して、以下の等式を示せ。

(5) 非負実数 に対し、 を から距離 以内にある点の集合とする。 このとき、 の面積 は、 の面積 と の全長 を用いて

と表せることを示せ。

Kai

(1)

(2)

(3)

There are following 4 possibilities:

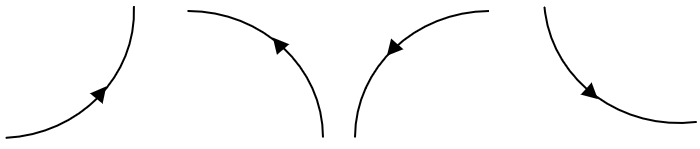
Case 1:

Case 2:

Case 3:

Case 4:

Therefore, for arbitrary we have .

(4)

Let . Then we have

Note that for time , tangent vector of is and unit normal vector is , hence

(5)

Note that the matrix in (4) is a Jacobian matrix. Consider the area () between and , we have

Since the area inside is , we have