東京大学 情報理工学研究科 2018年8月実施 数学 第3問

Author

etsurin

Description

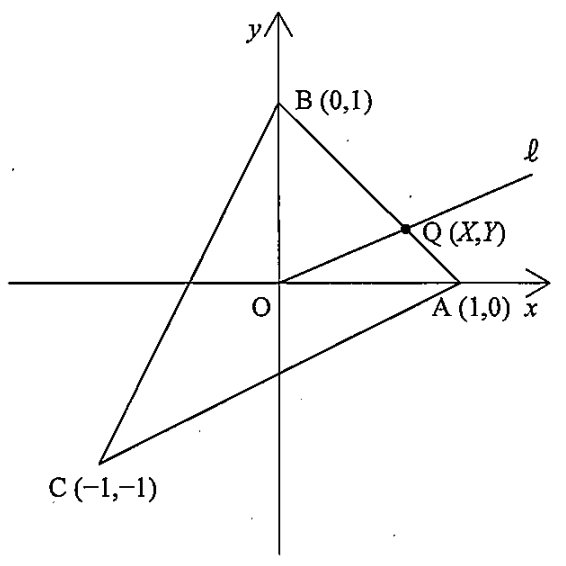
下図のように、平面上に三角形 が与えられており、各頂点の座標は 、、 とする。 原点 を端点とする半直線 をランダムに選ぶ。 すなわち、 を区間 上の一様分布に従う確率変数として

とおく。この半直線 と三角形 の周との交点を とおく。 また、 の座標を とおく。ただし、 は確率変数である。 以下の問いに答えよ。

(1) 点 が辺 上にある確率を求めよ。

(2) 点 が辺 上にあるという条件のもとでの の期待値は であることを示せ。 ただし、三角形 が直線 に関して対称であることを利用してよい。

(3) 点 が辺 上にあるという条件のもとでの の確率密度関数を、変数変換の公式

を使って求めよ。 ただし、 は任意の実数とし、 と はそれぞれ と の確率密度関数を表し、 は を満たす関数とする。

(4) 点 が辺 上にあるという条件のもとでの の期待値を とおく。 設問 (3) の結果を使って を求めよ。

(5) の期待値 を求めよ。

Kai

(1)

在 上，对应

(2)

在 上的条件下， 的条件分布

对应边 。转化为极坐标 。

(3)

在 上的条件下， 的条件分布

对应边 。转化为极坐标 。

(4)

, 则 。。

(5)

对应边 , 设 边上 的期待值为 。注意到 关于直线 对称。即 关于直线 对称。

令 , 这里 是分段函数， 对应边 三条边上时的情况。