跳到主要内容

東京大学 情報理工学系研究科 コンピュータ科学専攻 2024年8月実施 専門科目 問題1

Author​

vv (co-authored with GPT 5.2 extended thinking, finalized by 祭音Myyura)

Description​

とする． 上の言語 に対して，言語 を以下によって定義する．

例えば， ならば， である．以下の問いに答えよ．

(1) を正規表現 で表される言語とする． を正規表現として表せ．

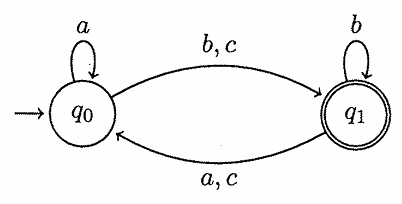
(2) 以下の有限オートマトンによって受理される言語を とする．ただし，初期状態は であり，受理状態の集合は である． を受理する状態数最小の決定性有限オートマトンを構成せよ．

(3) 以下の命題 1 が真であるか否かを答え，真であればその証明を，そうでなければ簡単な説明とともに反例を示せ．

  • 命題 1: 上のすべての正規言語 について， も正規言語である．

(4) 以下の命題 2 が真であるか否かを答え，真であればその証明を，そうでなければ簡単な説明とともに反例を示せ．

  • 命題 2: 上のすべての文脈自由言語 について， も文脈自由言語である．

Kai​

(1)​

先把 的形状写清楚：任意 都可写成

因此 中的字母 恰好出现两次（中间一次、末尾一次）。

若 ，设 中 的个数为 。则

所以 。又因为 以 “” 结尾，所以第二个 也以 “” 结尾，从而 必须以 “” 结尾。结合 ，可知 唯一的 就是在末尾，于是

另外 还要求整个串以 开头，所以 也必须以 开头。

再看 中“中间那次 ”的位置：在 中第一处 必然出现在第一个 的末尾（因为 唯一的 在末尾），所以该 正好落在两个 的拼接边界处。于是第一个 必须形如

并且为了末尾是 ，这里的 必须以 结尾，即 。令 （其中 ），则

反过来，任意 （）都有

所以都属于 。

因此

用正则表达式表示为

(2)​

先总结原 DFA 的关键性质（从图直接读出）：

  • 读到 ：无论在 还是 ，都会到 （相当于“重置到 ”）。
  • 读到 ：无论在 还是 ，都会到 （“重置到 ”）。
  • 读到 ：在 间切换（“翻转”）。

对任意串 ，令它在状态集合 上诱导的状态变换为

那么

注意：一旦 中出现过 或 ，最后一次出现的 会把状态“重置”为常量（全映到 或全映到 ），之后末尾若干个 只会在这两个常量间来回翻转。因此：

  • 若 不含 ，即 ，则 是“恒等”(k 偶)或“交换”(k 奇)，都满足 ，所以不在 。
  • 若 含有 或 ，则 必为常量变换：要么把两状态都送到 ，要么都送到 。只有当 是“常量 ”时，才有 。

所以

读完后，无论从还是出发都到

把它翻译成“末尾结构”的条件：设 的最后一个属于 的字母为 ，其后有 个 （即 且之后不再有 ）。

  • 若 ，读到 重置到 ，再读 个 翻转 次；要最终在 ，需 为偶数。
  • 若 ，读到 重置到 ，再读 个 ；要最终在 ，需 为奇数。

并且必须“出现过 或 ”（排除纯 ）。

接下来构造最小 DFA。只需要记住三种情况：

  • ：至今还没见过 或 （只读到若干个 ）。这是初态，非接受。
  • ：已经见过 ，但当前处于“拒绝型”（对应“末尾情况不满足”）。
  • ：已经见过 ，且当前处于“接受型”（对应“末尾情况满足”）。这是唯一接受态。

转移规则由上面的“重置/翻转”直接给出：

  • 从 ： 仍在 ；读到 进入拒绝型 ；读到 进入接受型 。
  • 从 ： 读 重置回 ；读 重置到 ；读 会翻转到 。
  • 从 ： 读 重置到 ；读 留在 ；读 翻转到 。

用转移表表示（字母表 ）：

状态
（初态）
（接受态）

这台 DFA 的接受态集合为 。

最小性说明：三状态不可再合并。因为

  • （停在 ）不被接受，但串 （停在 ）被接受，故 。
  • 串 （停在 ）不被接受，但 被接受，且 不被接受，故 。
  • 与 一个拒绝一个接受，显然可区分。

因此最少需要 3 个状态，上述构造即为最小 DFA。

(3) 结论：真​

设 是正则语言，被某个 DFA

识别。对任意串 ，定义它在状态集合上的“整体迁移函数”

那么

关键点： 只是 到 的函数，而 有限，因此所有函数 的集合

是有限集合（大小为 ）。

据此构造一个新的 DFA 来识别 ：

  • 状态集合：（所有函数 ）。
  • 初态：恒等函数 （对应空串的迁移）。
  • 读入一个字母 时的更新：令 （单字母的迁移），则 . 这样读完 后， 恰为 。
  • 接受态集合：.

于是对任意 ， 读完 后所在状态为 ，而接受条件正是 ，等价于 。因此 。

由于 是有限自动机（状态数有限）， 是正则语言。命题 1 成立。

(4) 结论：假​

给出一个上下文无关语言 ，使得 不是上下文无关语言。

取

也就是

说明 是 CFL：

是 CFL（例如文法 ）；

也是 CFL（例如 ）；

而 CFL 对连接封闭，所以 为 CFL。

接下来证明 不是 CFL。考虑正则语言

若 是 CFL，则由于 CFL 与正则语言交仍为 CFL， 也应是 CFL。

我们计算 。设 ，则

那么

断言：对这类 ，有

理由如下。

  • 若 ，则存在分割 使得 ，。因为 必须先读完一段 再读 。在 的开头， 是一整段 。若 ，则在读完 后下一个符号仍是 ，不可能开始 。所以必须 。同理，为了让 的 紧接在这 之后，必须正好消耗掉开头的全部 ，因此还要 。否则 会导致 进入 前还残留或不足 ，无法匹配。于是 ，并且此时 只能是 （）。若 ，则 将以 开头，但 的串必须形如 ，不能以 开头，因此必须 。所以分割点被迫落在两个拷贝之间：，。现在 要求其后半部分 满足 。结合 ，得到 。
  • 反过来，若 ，则 显然可取 ，，所以 。

因此对于 ，

也就是说

而 是经典的“非上下文无关语言”。于是 不是 CFL，矛盾。

所以 不可能是 CFL。命题 2 为假。

目录