東京大学 情報理工学系研究科 コンピュータ科学専攻 2015年2月実施 問題2

Author

kainoj, 祭音Myyura

Description

Let us consider nondeterministic finite automata (NFA) and deterministic finite automata (DFA) over the alphabet . For example, the NFA shown below

recognizes the language

Here denotes the set of words over .

Answer the following questions.

(1) Present an NFA, with at most four states, that recognizes the language

Here denotes the length of the word .

(2) Present a DFA that recognizes the language in Question (1).

(3) A DFA that recognizes the language has no less than states. Prove this fact.

(4) Argue for the following statement:

• To recognize the same language, a DFA possibly needs the number of states that is exponentially bigger than an NFA does.

Kai

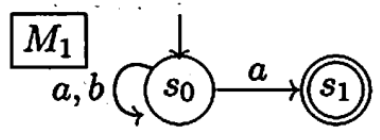
(1)

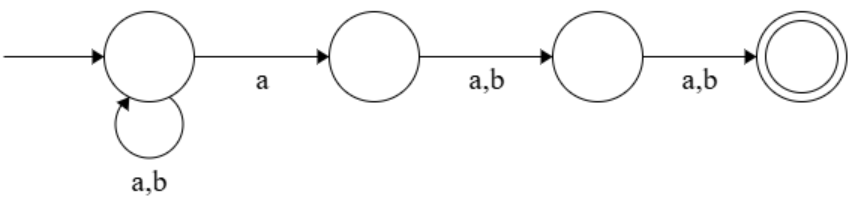
(2)

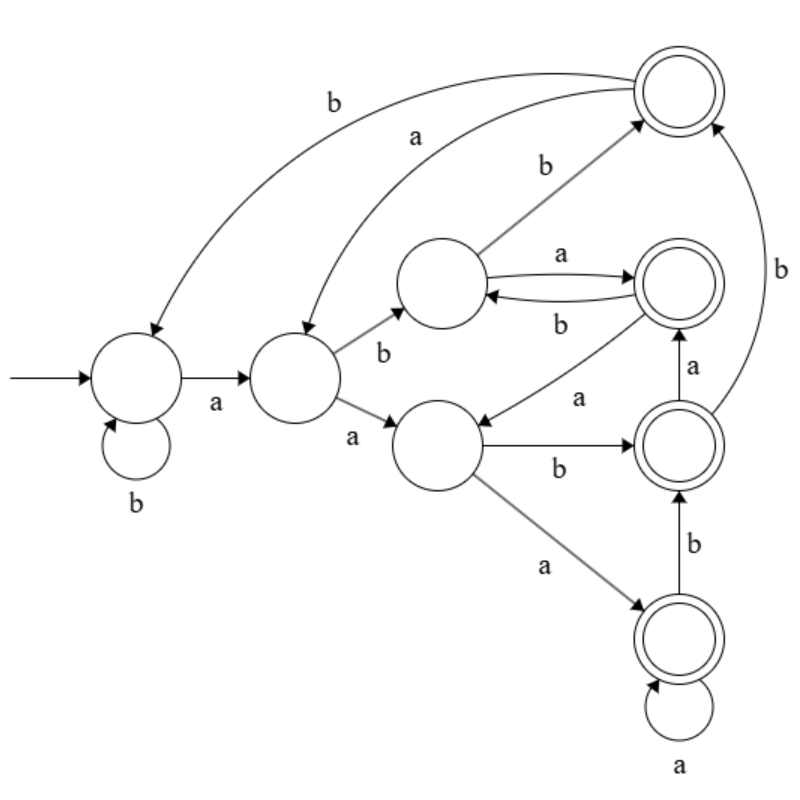
(3) + (4)

I'll prove that DFA that recognizes :

has no less than states. This is almost a copy-paste from Introduction to Automata Theory, Languages and Computation 3rd ed., Chapter 2.3.6.

Intuitively we need states to remember every possible ending of length : we can encode it as a binary string of length . Now, I'll show that there's no such DFA with less than states.

Suppose that there's DFA recognizing with less tan states. If so, then tere must exist a state in which is after reading two different sequences, say and . Since they are different, let be the last position on which they differ. By symmetry, assume that and .

• if , then and . Which means that state is both accepting and non-accepting.
• if , then we can append 's to both and . Then a state in which is after reading and is both accepting and non-accepting.

In both cases we get lead to contradiction. Thus, DFA recognizing has at least states.

• (3): Let . Then DFA recognizing has no less than states.
• (4): NFA recognizing has exactly states. Equivalent DFA has states.