跳到主要内容

ci_202208_programming_2

Author​

Description (English)​

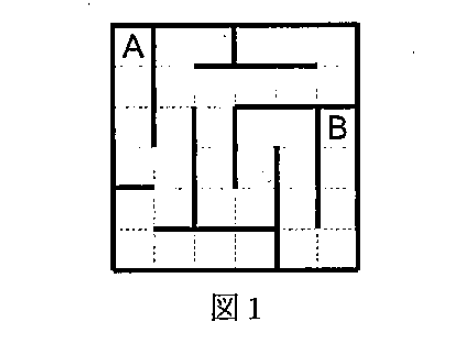
Suppose that we have a maze on a square board with cells. The cell in the -th row and the -th column is denoted by , where and . For example, Figure 1 shows a maze on cells. The cell A is and the cell B is .

fig2

When a sequence of numbers is stored, we store a character string in a file as follows.

2,0,13,0,1,6,8,1

This denotes the sequence of numbers where the 0th number is 2, the 1st number is 0, the 2nd number is 13, ... All the elements in a sequence are integers more than or equal to zero.

(1) A sequence of numbers {} is stored in file sequence.txt. Write down the 216-th element in that sequence on the answer sheet. Furthermore, write down the maximum number among the elements in that sequence on the answer sheet.

(2) Make a maze on cells in accordance with the following instructions. A sequence of numbers is stored in file p.txt. Its elements are either 0, 1, 2, or 3.

  1. Put walls along the outer limits of the maze.
  2. For every pair of and , where and ,
    • put the upper wall for cell when is 0,
    • put the left wall for cell when is 1,
    • put the lower wall for cell when is 2,
    • put the right wall for cell when is 3.

Here, and is the -th element of the sequence of numbers . Note that, for different pairs of and , the same wall may be put.

(2-a) Write down on the answer sheet the existence of the upper, lower, left, and right walls for cells , , and in this maze.

(2-b) Write down on the answer sheet the number of the L-shaped corner cells in this maze. A cell is a L-shaped corner cell when it is surrounded with exactly two walls directly jointed to form L-shape.

(3) Make a maze on cells in accordance with the following instructions. The start is cell and the goal is cell . A cell surrounded with four walls is called a closed cell.

  1. Put the upper, lower, left, and right walls for all the cells so that all the cells are closed cells.

  2. Set the current position to the start cell.

  3. Select a closed cell N in the maze among the upper, lower, left, and right cells adjacent to the current position. Then remove the wall separating the selected cell N and the current position. Move the current position to that cell N. Repeat this again.

    When selecting the cell N, refer to the sequence of numbers stored in file neighbor.txt. The elements of this sequence is either 0, 1, 2, or 3.

    Suppose that the current position is . Let be the -th element of the sequence . For given , when is 0, select the upper cell of the cell . When it is 1, select the left cell. When it is 2, select the lower cell. When it is 3, select the right cell for N, respectively. Here, . Choose for selecting N. is an integer more than or equal to zero and also is the minimum integer such that a closed cell is selected for N.

    When no cell is selectable for N, select a cell C. The cell C must not be a closed cell. Furthermore, at least one adjacent cell to C must be a closed cell. Move the current position to that cell C. When a necessary element of the sequence does not exist, select a cell C and move the current position to that cell C.

    When selecting the cell C, refer to the sequence of numbers stored in file cell.txt. Its elements are integers less than 40 and more than or equal to zero.

    Suppose that the current position is . Select a cell such that is minimum among the cells satisfying the requirements for C. Here, and is an integer more than or equal to zero.

    When no cell is selectable for C, the maze is completed. When a necessary element of the sequence does not exist, the maze is also completed.

(3-a) Write down on the answer sheet the existence of the upper, lower, left, and right walls for cells , , and in this maze.

(3-b) Write down on the answer sheet the number of the L-shaped corner cells in this maze. A cell is a L-shaped corner cell when it is surrounded with exactly two walls directly jointed to form L-shape.

(3-c) Find the longest straight passages in this maze and write their length down on the answer sheet. Furthermore, write down the number of such longest passages on the answer sheet. For example, the path between cells and in Figure 1 is a straight passage and its length is 5, which is the number of its cells. For the maze in Figure 1, a passage with length 5 is the longest and there are two such passages.

(3-d) We can reach the goal of this maze when proceeding through the maze by always keeping one wall on the left-hand side in the direction of the move. Write down on the answer sheet the number of the cells visited on the way to the goal. When the same cell is visited twice, that cell is counted only once. Include the start and the goal cells in the cells visited on the way. At first, the upper wall of the start cell is on the left-hand side in the direction of the move.

目录