東京大学 情報理工学系研究科 創造情報学専攻 2006年8月実施 プログラミング
Author
Description (日本語)
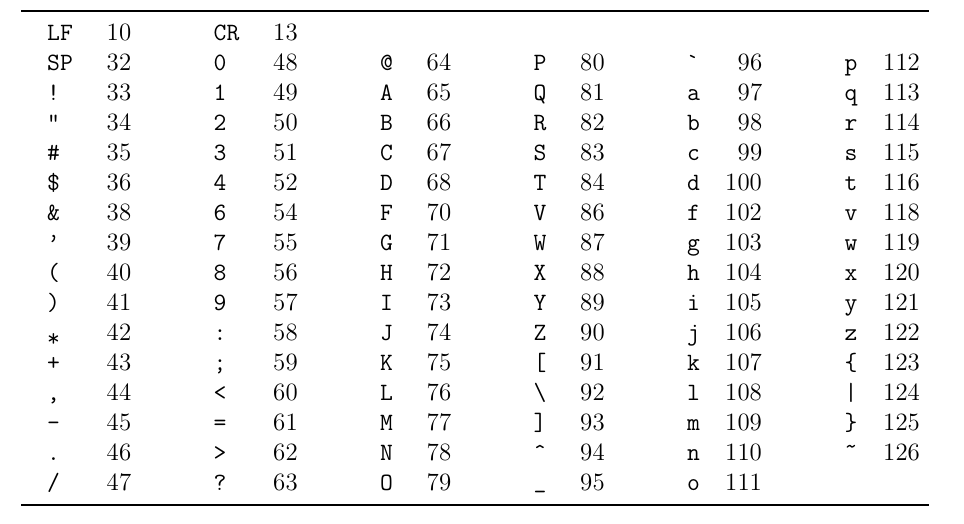
必要なら最後の ASCII コード表を使いなさい. この問題で扱う文字コードは 32～126 と改行に関するコードの計 96 種類のみである. また, 以下で使うファイルはすべて ASCII 文字で, 1 行 76 文字以内である.
問 1 鍵として指定した数だけ, アルファベットの英字を循環的に後ろへシフトする非常に単純な暗号 (シーザー暗号) がある. 鍵は 1～25 の整数である. 例えば, 鍵が 4 の場合, Japan は Neter と暗号化され, 鍵が 25 の場合, IBM は HAL と暗号化される. なお, 簡単のため, ここでは, 英字の大文字は大文字に, 小文字は小文字に変換されるとし, 空白や改行, 数字, 句読点などの記号は暗号化しない.
ファイル q1.txt を入力して解読しなさい. すなわち, 暗号化に使われた鍵を推測し, 元の英語の文章を復元しなさい.
問 2 問 1 のシーザー暗号はあまりにも単純すぎるので, 英字を別の英字に 1 対 1 変換する表 (換字表) を鍵とする暗号化もよく使われた.
2-1 ファイル q21.txt に数万文字の英語の文章がある. 出典は以下の通り.
The 1980 ACM Turing Award Lecture by Charles Antony Richard Hoare The Emperor’s Old Clothes, Communications of the ACM, Volume 24, Number 2, 1981. Copyright 1981, Association for Computing Machinery, Inc.
www.braithwaite-lee.com/opinions/p75-hoare.pdf
このファイルに含まれる英字の出現頻度 (出現回数) を求めなさい. ただし, 英字の大文字は小文字に含めて数える. その結果を出現頻度の大きい順に並べたものを表示するプログラムを書きなさい. 表示は英字 (大文字は小文字で代表) と出現頻度が対になっていればどんな形式でもよい.
2-2 ファイル q22.txt に, ある換字表を使って暗号化された文章が入っている. ここでは簡単のため, 英字以外は変換せず, 英字の大小はそのままになっている. 換字表による文字変換プログラムと, 英語の知識にもとづく試行錯誤を行なって, この暗号文の解読を試み, 得られた平文をファイル a22.txt に出力しなさい.
(出典 www.cs.utexas.edu/users/EWD/transcriptions/EWD03xx/EWD340.html)
問 3 換字表による暗号化は, 平文の文字出現頻度分布がヒントになるので, 解読されやすい. しかし, 暗号化する前の文のどの文字もほぼ同じ出現頻度になっていれば, 解読は困難になる. 出現頻度の高い文字には短い 2 進列, 出現頻度の低い文字には長い 2 進列を割り当てる符号化を行なうと, 2 進列のパターンの出現頻度がほぼ同じになる. すなわち, テキストの圧縮を行なってから暗号化すると, 解読は難しくなる.
3-1 q21.txt における 96 種類すべての文字の出現頻度を求め, すべての文字を出現頻度の高いものほど短い 2 進列で表わす符号化を考えよう. 以下にそのような符号化の考え方 (ハフマン符号化) を示す. これをプログラムしなさい. 文字と対応する 2 進列がわかるように出力されていれば, 出力形式はなんでもよい. 空白は SP, 改行は NL と表示しなさい.
符号化の考え方: まず, 図 1(4) のように, すべての文字が葉であるような順序付き 2 進木を構成する. 文字に対する符号を求めるには, 根から葉へ木をたどり, 左側の分岐をたどったら 0,右側の分岐をたどったら 1 と順に 0, 1 を振っていく. 葉に到達するまでに得られた 0, 1 の列がその文字に対する符号である. 例えば, 図 1(4) では B は 100 と 2 進符号化される.
ハフマン符号を得るための順序付き 2 進木の作り方: 次のようにボトムアップに構成する.
- 出現頻度表のすべての文字を節点とし, それぞれの節点に, 頻度表に書かれた出現頻度を値として与える. ここでは, 頻度 0 の文字は存在しない.
- まだ親をもたない節点の中で最も小さな値をもつ節点と, 次に小さな値をもつ節点をそれぞれ右の子, 左の子とする節点を生成し, その節点には 2 つの子の値の和を値として与える. これを 2 進木が完成するまで繰り返す. 値が等しいものがあった場合は, 文字同士なら, ASCII コードの小さいほうが右, また, 節点は新しくつくられたもののほうが右という規則にする.
図 1 に A, B, C, D, E の頻度がそれぞれ 50, 20, 33, 15, 40 だった場合の組み立て方を示した.
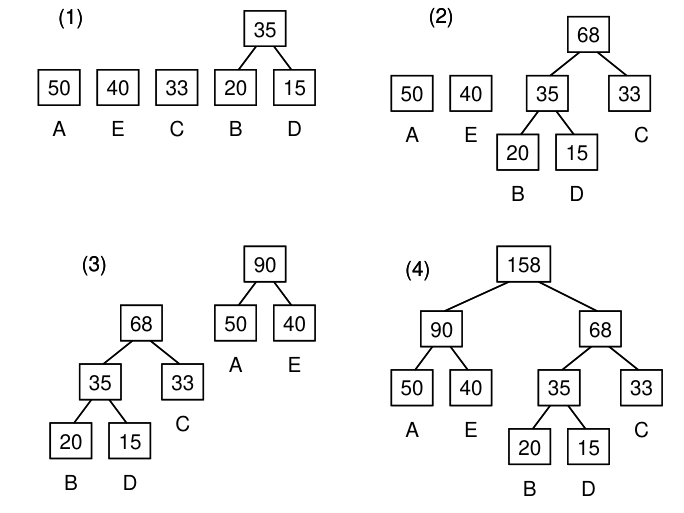
図 1. ハフマン符号化のための順序付き 2 進木のつくりかた (例)
3-2 これまで扱ってきた NL (改行) を含めた 96 種類の文字に対して, 頻度を考えずに 2 進数に符号化すると, 1 文字あたり平均 6.5 ビットを要する. 上で求めたハフマン符号化の 2 進数のビット数は 1 文字当たり平均何ビットになるか, 少なくとも小数点以下 2 桁まで計算するプログラムを書きなさい. ただし, このときの平均は文字の出現頻度の重みをつけること.
Description (English)
Refer to the ASCII code table on the last page, if necessary. The number of character codes dealt with in this examination will be 96; that is, from 32 to 126 and that for newline. Files consist of ASCII characters. Every line has no more than 76 characters.
Q1 Caesar cipher is one of the simplest cipher which shifts alphabet letter by Japan is enciphered into Neter, and if the key is 25, IBM is enciphered into HAL. Here we preserve uppercase and lowercase of alphabet letters, and do not substitute any other characters such as space, digits, and punctuation marks. Decipher the Caesar cipher text in the file q1.txt. Namely, infer the key and recover the original English sentences.
Q2 Caesar cipher is too simple to defense against cipher breaking. A little complicated cipher uses a substitution table which substitutes each letter by another letter. The substitution table gives a one-to-one mapping within the alphabet.
2-1 The file q21.txt is an article consisting of about ten thousand words. The text is cited from:
The 1980 ACM Turing Award Lecture by Charles Antony Richard Hoare The Emperor’s Old Clothes, Communications of the ACM, Volume 24, Number 2, 1981. Copyright 1981, Association for Computing Machinery, Inc.
www.braithwaite-lee.com/opinions/p75-hoare.pdf
Compute the frequencies (or occurrence counts) of all alphabet letters in this text, counting uppercase alphabet letters as their corresponding lowercase letters. Make a program that outputs the result in the descending order of frequency. You can choose arbitrary output format under the condition that each alphabet letter in lowercase is paired with its occurrence count.
2-2 The file q22.txt is a cipher text made by using a certain substitution table, where characters other than alphabet letters are unchanged for simplicity. Break the cipher by using an appropriate character substitution program and some trial and error inference. Output the full deciphered text on a file named a22.txt.
This article is cited from: www.cs.utexas.edu/users/EWD/transcriptions/EWD03xx/EWD340.html.
Q3 As you can see, ciphers based on a simple substitution table are easily broken with a hint of alphabet letter frequency distribution. If the frequency distribution of the characters of the original text becomes flat, it would be more difficult to break. For the preparation, let us consider an encoding scheme in which a short binary code is assigned for a frequently occurring character and a long binary code for an infrequently occurring character. In such an encoding, every binary pattern tends to appear in the same probability. We can readily imagine the code breaking would be much more difficult if we compress the original text before enciphering.
3-1 Compute the frequencies of all 96 characters in q21.txt and program the Huffman coding in which more frequent characters have shorter binary codes, as shown below. Output the encoding table in which each character is paired with the corresponding binary code, namely, sequence of 0 and 1. You can choose your convenient output format, but space character and newline character should be denoted SP and NL, respectively.
Code assignment: First, you have to make an ordered binary tree as shown in Figure 1(4), each of whose leaves represents a character. To assign a code to a character, start from the root toward the corresponding leaf. In the course, you get 1 if you choose the left branch, and 0 if the right branch. The 0-1 sequence from the root up to the leaf is the code for the character. For example, the Huffman code for the character B in Figure 1(4) is 100.
Construction of an ordered binary tree for Huffman code: Make a tree in a bottom-up manner as described below.
- Create a node for each character in the frequency table, and give the frequency as its value. Note that there is no character of zero occurrence in this problem.
- Until a complete binary tree is constructed, create a parent node of the two nodes that have not yet a parent, each of which is one that has the least value, and the other that has the second least value. The node of the least value will be the left child of the new node, and the node with the second least value will be the right child. If the least value equals to the second least value, newer node will be the right child, and character node with smaller ASCII code will be the right child if both are character nodes. Figure 1 illustrates the tree construction, where five characters A, B, C, D, and E have frequencies 50, 20, 33, 15, and 40, respectively.
Figure 1. Construction of an ordered binary tree for Huffman coding (example)
3-2 You can see that we need 6.5 bits on an average for 96 characters if we do not consider their frequencies. Compute the average number of bits for binary code for 96 characters you made in the Question 3-1, at least up to 2 places of decimals. Note that the average should be weighted by each character frequency.
Kai
The sample data file of q1.txt are here.
Sxx, jzf dppx ez slgp qzfyo esp qzwwzhtyr dpypepynpd.
Zyp zq esp dtxawpde pilxawpd zq l dfmdetefetzy ntaspc td esp Nlpdlc
ntaspc, hstns td dlto ez slgp mppy fdpo mj Ufwtfd Nlpdlc ez
nzxxfytnlep htes std lcxj. Nlpdlc td nzydtopcpo ez mp zyp zq esp qtcde
apcdzyd ez slgp pgpc pxawzjpo pyncjaetzy qzc esp dlvp zq dpnfctyr
xpddlrpd. Nlpdlc opntopo esle dstqetyr plns wpeepc ty esp xpddlrp
hzfwo mp std delyolco lwrzctesx, lyo dz sp tyqzcxpo lww zq std
rpypclwd zq std opntdtzy, lyo hld es
We currently do not have OTHER corresponding sample data files. If you have them and are willing to share, please submit a PR.