東京大学 情報理工学系研究科 創造情報学専攻 2005年8月実施 筆記試験 第3問

Author

itsuitsuki

Description

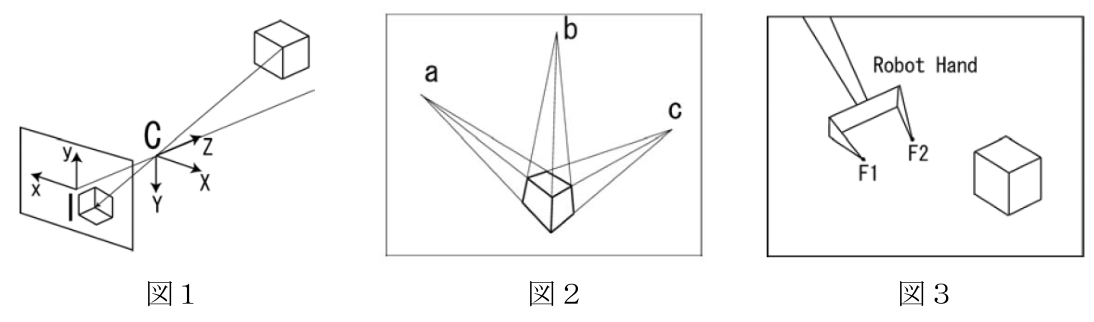
図1に示すように，三次元空間中の物体の光が一点C(光学中心)を通って撮像面に投影されるピンホールカメラを考える．光学中心から撮像面へ垂直に引いた直線は光軸と呼ばれ，撮像面と光軸の交点は画像中心と呼ばれる．図1に示すように，光学中心に三次元のカメラ座標系 C-X,Y,Z をとり，画像中心に二次元の画像座標系 I-x,y をとる．光学中心から撮像面までの距離をfとした場合に，三次元空間の点 の投影面上の点 の座標は次のように表される．

以下の問に答えよ．

(1) 三次元空間中の直線Lの無限遠点が撮像面に投影される点はLの消失点と呼ばれる．点 を通り，方向ベクトル に沿う直線L上の点 の座標を表し，直線Lの消失点の座標 を求めよ．

(2) 図2のように直方体が投影されている画像上で直方体の平行線の消失点 , , の間にはどういう関係式が成立するか示せ．

(3) 直方体が投影されている投影面の映像が濃淡画像として得られるとして，直方体の稜線を濃淡画像の中から得る画像処理について説明せよ．

(4) 図3はロボットの基準座標系で定義される位置と姿勢を指定することでその場所へ動かすことができるロボットハンドの投影像を示す．ロボットハンドの指先F1, F2の投影面上の運動軌跡を画像処理によって得られるとする．直交する3つの方向にロボットハンドを動かして，ロボットの基準座標系からカメラ座標系への変換行列を得る方法を考える．3つの消失点座標に加えて，他にどのような情報が必要となるか説明せよ．

Description (English)

Consider a pinhole camera model as shown in Fig. 1, where the light from an object in three dimensional (3-D) space goes to the screen through a single point C (optical center). The vertical line to the screen through the optical center is called the optical axis, and the point where the optical axis crosses the screen is called the image center. Set the 3-D Camera coordinate system C-X,Y,Z at the optical center and the two dimensional (2-D) Image coordinate system I-x,y at the image center as shown in Fig. 1. When the distance from the optical center to the screen is f and the 3-D point is projected to the 2-D point on the screen, the coordinates of are described as follows:

Answer the questions below.

(1) The point on the screen projected from the infinity point on a line L in 3-D space is called the vanishing point of L. When L goes through a 3-D point with an orientation vector , describe the 3-D coordinates of the point on L and calculate the coordinates of the vanishing point of L.

(2) Fig. 2 shows the projected image of a rectangular solid and three vanishing points , , of the parallel edge lines on the solid. Describe the equations that hold among the three vanishing points.

(3) When the projected image of a rectangular solid is given as a gray image, explain the method of image processing for getting the edge lines from the gray image.

(4) Fig. 3 shows an image of a robot hand controllable by specifying its position and orientation in the base coordinate system of the robot. Image processing provides the motion trajectories of the end points F1, F2 of the robot fingers on the screen. Consider the method to get the transformation matrix from the robot base coordinate system to the camera coordinate system by translating the robot hand in three orthogonal directions. Explain what kind of additional information other than the coordinates of three vanishing points is required to get the transformation matrix.