東北大学 理学研究科 地球物理学専攻 2022年8月実施 [7]

Author

Miyake

Description

(1) 次の微分方程式を解け。なお、問 (ii) は非自明解を求めること。

(2) 図１のように長径 、短径 の楕円に内接する長方形の面積の最大値を、ラグランジュの未定乗数法を用いて求めよ。ただし、 は正の定数とする。

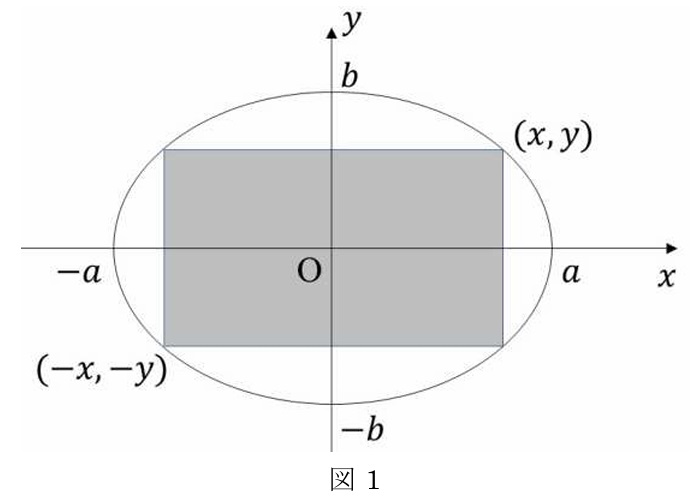
(3) とするとき、 であることを示せ。ただし、 は正の定数とする。

(4) ある部品を使い始めてから故障するまでの時間 が指数分布 に従うとする。ただし、, とする。

• (i) 部品を使い始めてから時間 までに故障が起こらない確率を求めよ。
• (ii) 部品を使い始めてから時間 まで故障が起こらなかったと条件の下で、その後、時刻 までの間に故障が起こる確率を求めよ。
• (iii) 部品を使い始めてから故障するまでの平均時間を求めよ。

Kai

(1)

(2)

楕円に内接する長方形の頂点の座標を ただし とすると、

が成り立ち、長方形の面積は

である。

そこで、ラグランジュの未定乗数 を導入して、

とおき、

とおく。

式 (), (), () から

が得られるので、求める最大値は

である。

(3)

(4)

(i)

時刻 までに故障する確率は

であるから、求める確率は

である。

(ii)

(i) の を使って、求める条件付き確率は次のように計算できる：

(iii)