跳到主要内容

東北大学 工学研究科 電気・情報系 2023年2・3月実施実施 基礎科目 問題4 情報基礎2

Author​

祭音Myyura

Description​

以下の問に答えよ。

(1)​

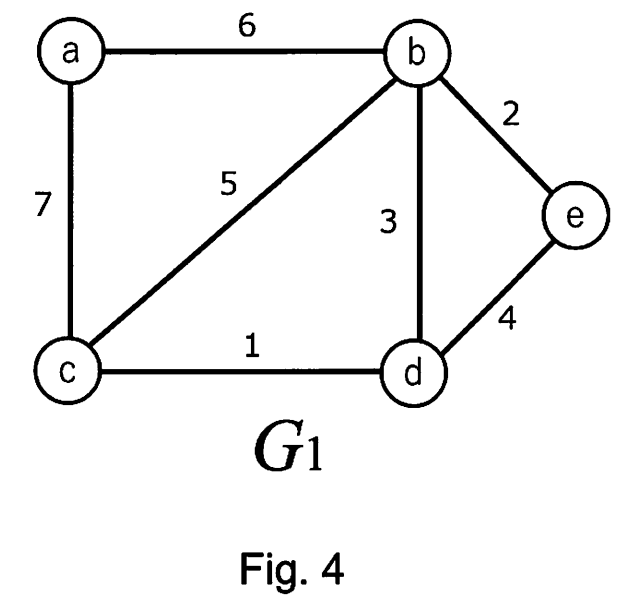
節点の集合 と重みが付いた枝の集合 からなる連結無向グラフ について考える. Fig. 4 のグラフ はそのような連結無向グラフの例であり、各枝の中央付近に記載の整数は、その枝の重みである。

(a) Fig. 4 のグラフ の隣接行列と隣接リストを示せ、ただし、枝の重みの情報は含まなくても良い。

(b) 個の節点と 個の枝からなるグラフ の隣接行列と隣接リストを格納するのに必要な記憶領域のサイズを 記法でそれぞれ示せ。

(c) グラフ の連結部分グラフの中で、 の全ての節点を含む木を の全域木と呼ぶ、また、 の全域木の中で、枝の重みの合計が最小であるものを の最小全域木と呼ぶ. Fig. 4のグラフ の最小全域木を示せ.

(2)​

各行の要素の値は左から右に昇順ソートされ、かつ、各列の要素の値は上から下に昇順ソートされている 行 列の整数行列 を考える、任意の整数 に対して、 に値が である要素が含まれる場合は「Yes」 を出力し、そうでない場合は「No」を出力する探索アルゴリズムを考える、時間計算量が となるような探索アルゴリズムの概要を説明せよ。

Kai​

(1)​

(a)​

隣接行列​

隣接リスト​

(b)​

  • 隣接行列は の行列で、各要素に辺の重み（整数）を格納するため、メモリ使用量は となります。
  • 隣接リストは各ノードに接続されているノードとその重みをリストで保持します。全辺数 を考えると、メモリ使用量は です。

(c)​

クラスカル法では以下の辺が選ばれることになります。

  • 重み 1
  • 重み 2
  • 重み 3
  • 重み 6

これで、最小全域木の重みの合計は です。

(2)​

アルゴリズム概要​

  1. 右上から開始する。ここでは右上 とする。
  2. ループ：
    • もし なら「Yes」を返す（終了）。
    • もし なら、この列の下方向はすべて 以上なので、列を1つ左へ移動（）。
    • もし なら、この行の左方向はすべて 以下なので、行を1つ下へ移動（）。
  3. インデックスが範囲外になったら要素は存在しないので「No」。

計算量​

行インデックス は最大 回増え，列インデックス は最大 回減る。したがって比較回数は高々 ，時間計算量は 。

目录