跳到主要内容

東北大学 工学研究科 電気・情報系 2015年8月実施 問題4 情報基礎2

Author​

祭音Myyura

Description​

日本語版​

下記の条件を満たす 分木を、 分探索木と呼ぶ、

  • (条件) 各節点 に対し、 の要素を とするとき、 の左部分木内の要素はすべて より小さ く、 の右部分木内の要素はすべて さより大きい。

各節点の要素とは重複しない整数であるとし、以下の問に答えよ。

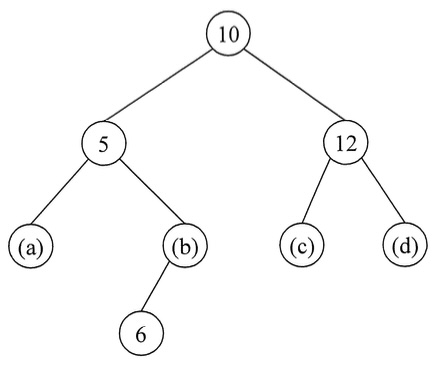
(1) Fig. 4 は空の 分探索木に を順に挿入して得られた 分探索木 を表している。要素 ，，， の値を示せ.

(2) Fig. 4 の から要素 を持つ節点を削除し、得られる 分探索木を示せ、なお、要素 ，，， について、問(1)で示した具体的な値を用いてよい。

(3) ある 分探索木から節点 を削除するアルゴリズムを与えよ。

(4) ある 分探索木のすべての要素を昇順に列挙する効率のよいアルゴリズムを示せ。

English Version​

A binary tree that satisfies the following condition is called a binary search tree.

  • (Condition) For each node , let be the element of , each element stored in the left sub-tree of is smaller than , and each element stored in the right sub-tree of is greater than .

Assume that the element of each node is an unique integer. Answer the following questions.

(1) Fig. 4 shows a binary search tree obtained by inserting integers to an empty binary search tree in this order. Show the values of elements and .

(2) Delete the node which stores the element from in Fig. 4, and show the obtained binary search tree. For the elements and , you can use the concrete values you give in question (1).

(3) Give an algorithm to delete a node from a binary search tree.

(4) Describe an efficient algorithm to enumerate all elements of a binary search tree in ascending order.

Fig. 4

Kai​

(1)​

  • 2
  • 8
  • 11
  • 15

(2)​

        8
     /     \
    5      12
  /   \   /   \
 2     6 11   15

or

       11
     /    \
    5      12
  /   \      \
 2     8      15
      /
     6

(3)​

func minValue(root)
    minv = root->key
    while root->left do
        minv = root->left->key
        root = root->left
    return minv

func deleteNode(root, key)
    if root == NULL then
        return root

    if key < root->key then
        root->left = deleteNode(root->left, key)
    else if key > root->key then
        root->right = deleteNode(root->right, key)
    else
        if root->left == NULL then
            return root->right
        elif root->right == NULL then
            return root->left

        root->key = minValue(root->right)
        root->right = deleteNode(root->right, root->key)

    return root

(4)​

Hint: The inorder traversal of a BST gives the values of the nodes in sorted order.

func inorder(root):
    if root != NULL then
        inorder(root->left)
        print(root->key)
        inorder(root->right)