跳到主要内容

大阪大学 情報科学研究科 情報工学 2016年8月実施 アルゴリズムとプログラミング

Author​

祭音Myyura

Description​

図 1 に示す ANSI-C 準拠である C 言語プログラムは、以下に挙げる 4 個の制約を満たす重み付き無向グラフ（weighted undirected graph） における 2 頂点（vertex）間の最短経路長（shortest path length）を出力するプログラムである。

  • 頂点数を として、頂点 の非負整数（non-negative integer）で識別できること。
  • すべての辺（edge）の重みが非負整数であること。
  • グラフ は連結（connected）であること、すなわち、任意の 2 頂点間に経路が存在する。
  • 無限大（infinity）とみなす値を INF として、任意の 2 頂点間の最短経路長が INF 未満であること。

ここで、始点（source） から終点（destination） への最短経路とは、 から への経路上の辺の重みの和（sum）が最小（minimum）となる経路であり、 と が同一頂点である場合、その最短経路長は である。 本プログラムは、グラフ の頂点数 を変数（variable）n に格納し、頂点 から頂点 への辺の重み を、配列（array）w の要素（element）w[i*n+j] に格納している。 なお、存在しない辺に対しては重みの値を INF とし、任意の頂点 に対して とする。図 2 に、図 1 で扱うグラフを示す。以下の各問に答えよ。

(1) 22〜34 行目の while 文の処理において 1 巡回および 2 巡回の終了時における Len[0] ~ Len[3] の値を、解答用紙の太線内の空欄を埋めることにより答えよ。

(2) 関数 compute が実現しているアルゴリズムの時間計算量（time complexity）のオーダ表記（order notation）を、頂点数を 用いて答えよ。その理由も簡潔に説明せよ。

(3) 最短経路長だけでなく、最短経路の一つを出力するように図 1 のプログラムを変更したい。例えば、始点 0 から終点 3 への最短経路であれば、以下のように出力したい。

Shortest Path Length from 0 to 3 is 3
- 0 - 1 - 3

そこで、5, 17, 27 および 47 行目の注釈を解除（uncomment）し、下記に示す関数 printpath の定義を 12 行目の位置に挿入した。 関数 printpath を呼び出して上記のような出力を得るためには、（ア）および（イ）をどのように記述すればよいか、適切な文をそれぞれ答えよ。

void printpath(int v) {
    if (v != -1) { printpath(Prev[v]); printf("- %d ", v); }
}

(4) 図 1 の main 関数を変更することにより、頂点数を に固定したときの一般のグラフにおけるすべての頂点対間（all-pairs of vertices）の最短経路長を出力したい。 その実現のために、44 行目以降に以下の変更のみを許す。

  • 関数 compute の呼び出しを追加・削除し、その実引数（actual argument）を変更してよい。
  • 関数 printf の呼び出しを追加・削除し、文字列や配列 Len の要素に限り、それらを出力してよい。

なお、処理対象のグラフに合わせて 38 ~ 41 行目の値は変更されているものとする。また、最短経路は出力しなくてよい。以下の各小問に答えよ。

  • (4-1) すべての頂点対間の最短経路長を出力するためには、関数 compute をどのように呼び出せばよいか、簡潔に説明せよ。呼び出し回数 の値に言及し、できるだけ の少ない方法を示せ。
  • (4-2) 22 行目を以下のように変更した。変更後の関数 compute をどのように呼び出せば、すべての頂点対間の最短経路長を出力できるか、簡潔に説明せよ。呼び出し回数 の値に言及し、できるだけ の少ない方法を示せ。
while (allvisited(visited, n)==0) {    →    while (visited[d]==0) {
            変更前                                  変更後
#include <stdio.h>
#define INF  255
#define MAXN 16

int Len[MAXN];    /*  int Prev[MAXN];  */

int allvisited(int *a, int n) {
    int i, r = 1;
    for (i = 0; i < n; i++) { r *= a[i]; }
    return r;
}

void compute(int *w, int n, int s, int d) {
    int i, j, next, min, visited[MAXN];

    for (i = 0; i < n; i++) {
        Len[i] = INF; visited[i] = 0;   /*  Prev[i] = -1;  */
    }

    i = s; Len[i] = 0; visited[i] = 1;

    while (allvisited(visited, n) == 0) {
        min = INF; next = d;
        for (j = 0; j < n; j++) {
            if (visited[j] == 1) continue;
            if (Len[j] > Len[i] + w[i*n+j]) {
                Len[j] = Len[i] + w[i*n+j];   /*  空欄 (ア)  */
            }
            if (min > Len[j]) {
                min = Len[j]; next = j;
            }
        }
        i = next; visited[i] = 1;
    }
}

int main() {
    int w[] = { 0,   2,   5,   INF,
                2,   0,   1,   1,
                5,   1,   0,   2,
                INF, 1,   2,   0   };
    int n = 4;

    compute(w, n, 0, 3);
    printf("Shortest Path Length from 0 to 3 is %d\n", Len[3]);

    /*  空欄 (イ)  printf("\n");  */

    return 0;
}

図１: 2 頂点間の最短経路長を出力するプログラム
​

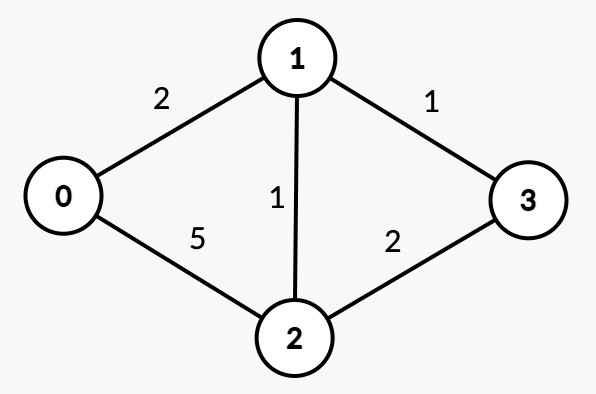
図２: 図１で扱うグラフ
​

Kai​

(1)​

1 巡回終了時における Len[0] ~ Len[3] の値: 0, 2, 5, 255

2 巡回終了時における Len[0] ~ Len[3] の値: 0, 2, 3, 3

(2)​

全ての頂点に対して 22〜34 行目の while 文の処理を行う必要があるので、計算量は である。

(3)​

  • 空欄 (ア): Prev[j] = i;
  • 空欄 (イ): printpath(3);

(4)​

(4-1)​

次のように呼び出せば良い。（）

compute(w, n, 0, 3);
printf("%d %d %d\n", Len[1], Len[2], Len[3]);
compute(w, n, 1, 3);
printf("%d %d %d\n", Len[0], Len[2], Len[3]);
compute(w, n, 2, 3);
printf("%d %d %d\n", Len[0], Len[1], Len[3]);
compute(w, n, 3, 3);
printf("%d %d %d\n", Len[0], Len[1], Len[2]);

(4-2)​

次のように呼び出せば良い。（）

int i, j;
for (i = 0; i < n; i++) {
    for (j = i + 1; j < n; j++) {
        compute(w, n, i, j);
        printf("%d\n", Len[j]);
    }
}
目录