名古屋大学 情報学研究科 情報システム学専攻 2024年8月実施 専門 問4

Author

祭音Myyura

Description

頂点の集合が 、辺の集合が の無向グラフを と表記する。 頂点 を端点とする辺は として表す。 この問題では，ループや多重辺を持たない単純グラフのみを考え，グラフに関する用語を以下のように定義する。

• が完全グラフ：異なる任意の頂点の組 に対し，辺 が存在する。
• が正則グラフ： の全ての頂点が同一の次数を持つ。頂点の次数とは，その頂点を端点に持つ辺の本数である。
• が の補グラフ： であり，異なる頂点の組 に対し， のとき，かつそのときのみ 。
• グラフ が と同型：次の性質を満たす全単射 が存在する； のとき，かつそのときのみ 。

(1) 頂点数 の完全グラフを示せ。

(2) 頂点数 の完全グラフが持つ辺の本数を答えよ。

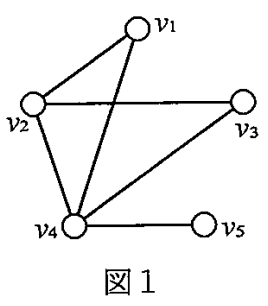
(3) 図 1 で与えられるグラフの補グラフを示せ。解答のグラフには頂点名を記すこと。

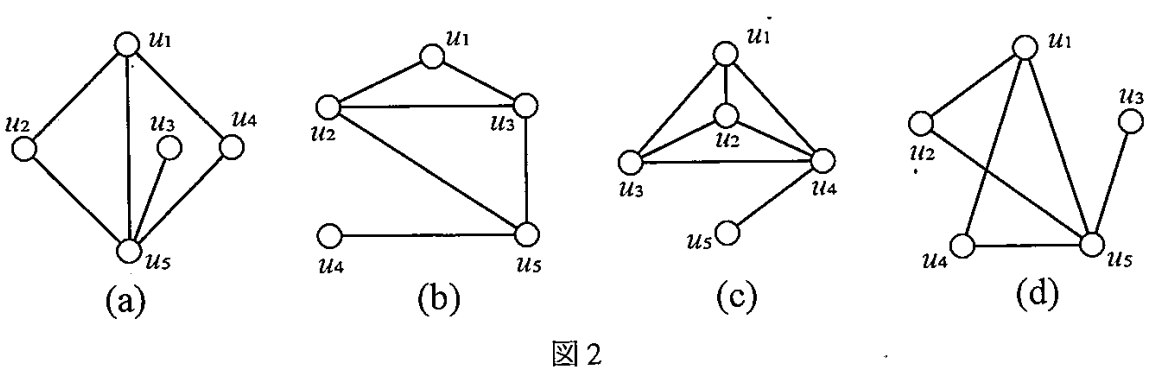
(4) 図 2 の から に示す 4 つのグラフのそれぞれについて，図 1 のグラフと同型であるかどうかを答え，同型の場合は頂点間の全単射を示し，同型でない場合は，同型でないと判断する理由を述べよ。

(5) グラフ が与えられ、頂点数が です。ここで、グラフ の補グラフが 自身と同型である場合、 の頂点数 は または の形で表されることを示す。ここで、 は非負整数です。

(6) 問題 (5) を踏まえて、グラフ が正則グラフ（すべての頂点の次数が同じ）であれば、頂点数 は必ず の形で表される。

Kai

(1)

(2)

頂点数 の完全グラフでは，異なる 頂点の組の数だけ辺がある。 これは組合せの数 に等しいので，辺の本数は

である。

(3)

図 1 のグラフの頂点はであり，図から読み取れる辺は

の 本である。

補グラフ は

となる。

(4)

まず，図 1 のグラフ の各頂点の次数を調べる：

• （ と接続）
• （ と接続）
• （ と接続）
• （ と接続）
• （ のみと接続）

したがって次数列（次数の多重集合）は である。

以下，各図との比較を行う。

---

図 2 (a) について、次の全単射 を考えると、図 2 (a) のグラフは図 1 のグラフと同型であることが分かる。

図 2 (b) についての次数を調べると，

となり，次数列は である。

図 1 の次数列は であり，一致しない。 次数列はグラフ同型では不変なので， のグラフは図 1 のグラフと同型ではない。

図 2 (c) についての次数を調べると，

であり，次数列は となる。 これも図 1 の次数列 と一致しないため， (c) のグラフも図 1 のグラフと同型ではない。

図 2 (d) について、次の全単射

をとると，図 2 (d) のグラフは図 1 のグラフと同型であることが分かる。

(5)

グラフ の辺の数は 、補グラフ の辺の数は とおくと、任意の2つの頂点の組み合わせ に辺が存在するので、次の関係が成立する。

と が同型であることから、 が得られるので、

は整数でなければならないため、 は または として表されることがわかる。

(6)

グラフ が正則で、グラフ も正則グラフである。グラフ のすべての頂点の次数が とおくと、

が得られる。 は整数でなければならないため、 は （奇数）として表される。(5) の結論により、 は として表されることがわかる。