九州大学 工学府 土木工学専攻 2021年8月実施 数学 (ALL)

Author

Miyake

Description

Kai

【問題 1】

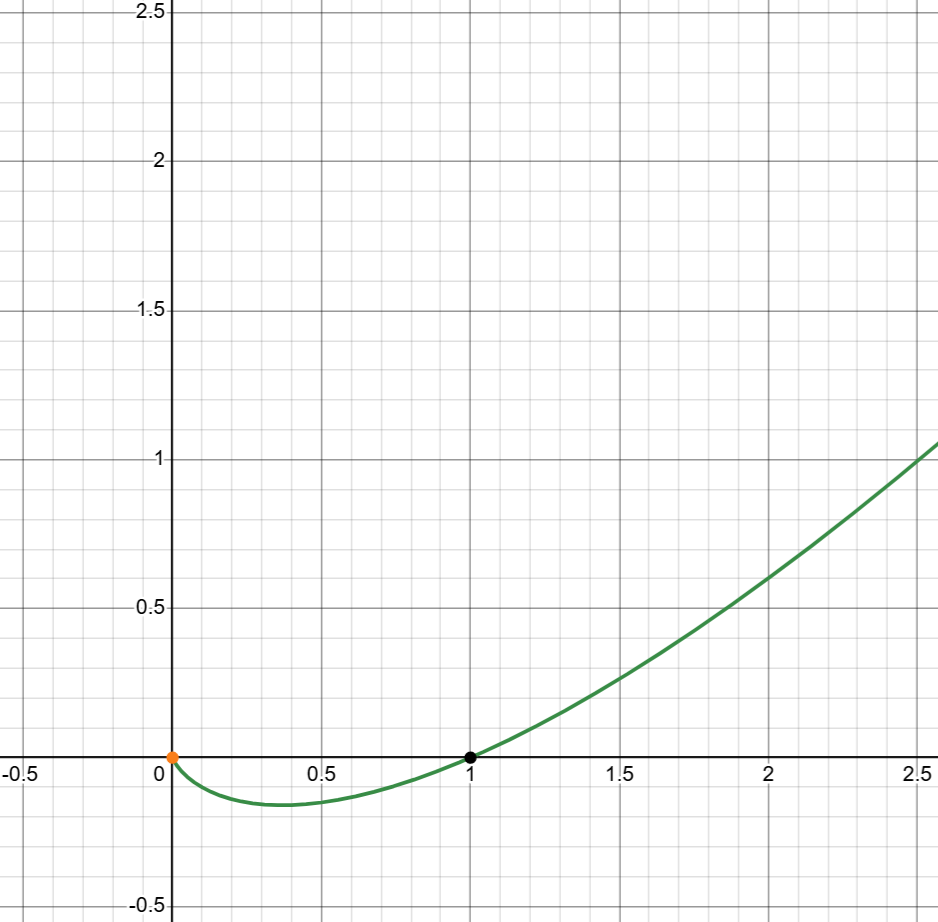
【問題 2】

(1)

曲面 上の点 を考えると、 の1次までで

であり、これらのベクトル積とその大きさは

である。 よって、

がわかる。

(2)

によって2次元極座標 を導入すると、 であり、次のように計算できる：

【問題 3】

(1)

を満たす関数 を求める。 式 () より、

なる関数 が存在することがわかる。 () を () に代入して整理すると、

を得る。 よって、求める一般解は

である。

(2)

式④が完全微分方程式であるための条件は、

なので、

を得る。

(3)

(2) の は今の場合、

であるから、

であり、積分因子として

を考えればよい。 このとき与えられた微分方程式は、

となり、 (1) と同じ方法を使って、一般解

を得る。

【問題 4】

(1)

(2)

4次の単位行列を とすると、

であり、まず、

がわかる。 また、

から、 について

がわかる。

(3)

の固有値は であるから、次のように対角化できる：

【問題 5】

平均は

であり、分散は

である。

【問題 6】

なので、求める95%信頼区間の下端は であり、 上端は である。