九州大学 システム情報科学府 情報理工学専攻・電気電子工学専攻 2023年8月実施 解析学・微積分

Author

Casablanca, Miyake

Description

(1) 積分

を計算せよ。ただし, を証明なしに用してよい。

(2) 次の微分方程式の一般解を求めよ。

(3) 複素関数 を考える。次の各問いに答えよ。

• (a) の極をすべて求めよ。

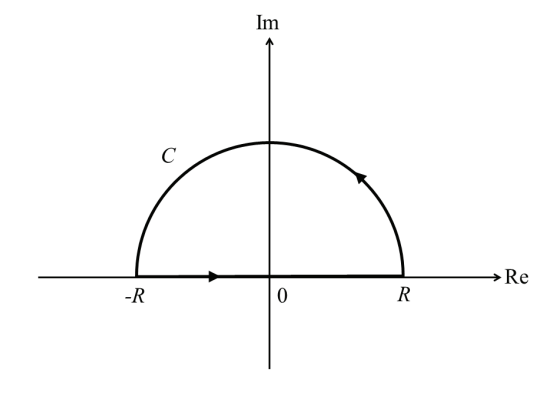
• (b) 下図に示す半円 に沿った複素積分 を求めよ。ただし, とする。

Kai - By Casablanca

(1)

(2)

where is a constant.

(3)

(a)

Consider ,

we get

and these are the poles

(b)

Kai - By Miyake

(1)

は偶関数であるから、

より、

がわかる。

とおくと、 であり、次のように計算できる：

(2)

の一般解は

である。このことを考慮して、与えられた微分方程式

に ( は の関数 ) を代入すると、

を得るので、求める一般解は

であることがわかる。

(3)

(a)

に ( は実数) を代入すると

であり、

となる。よって、 は

に1位の極をもつ。

(b)

(a) で求めた4つの極は

であるが、このうち の内側にあるのは である。

なので、 における留数は

であり、 における留数は

である。よって、留数定理より

がわかる。