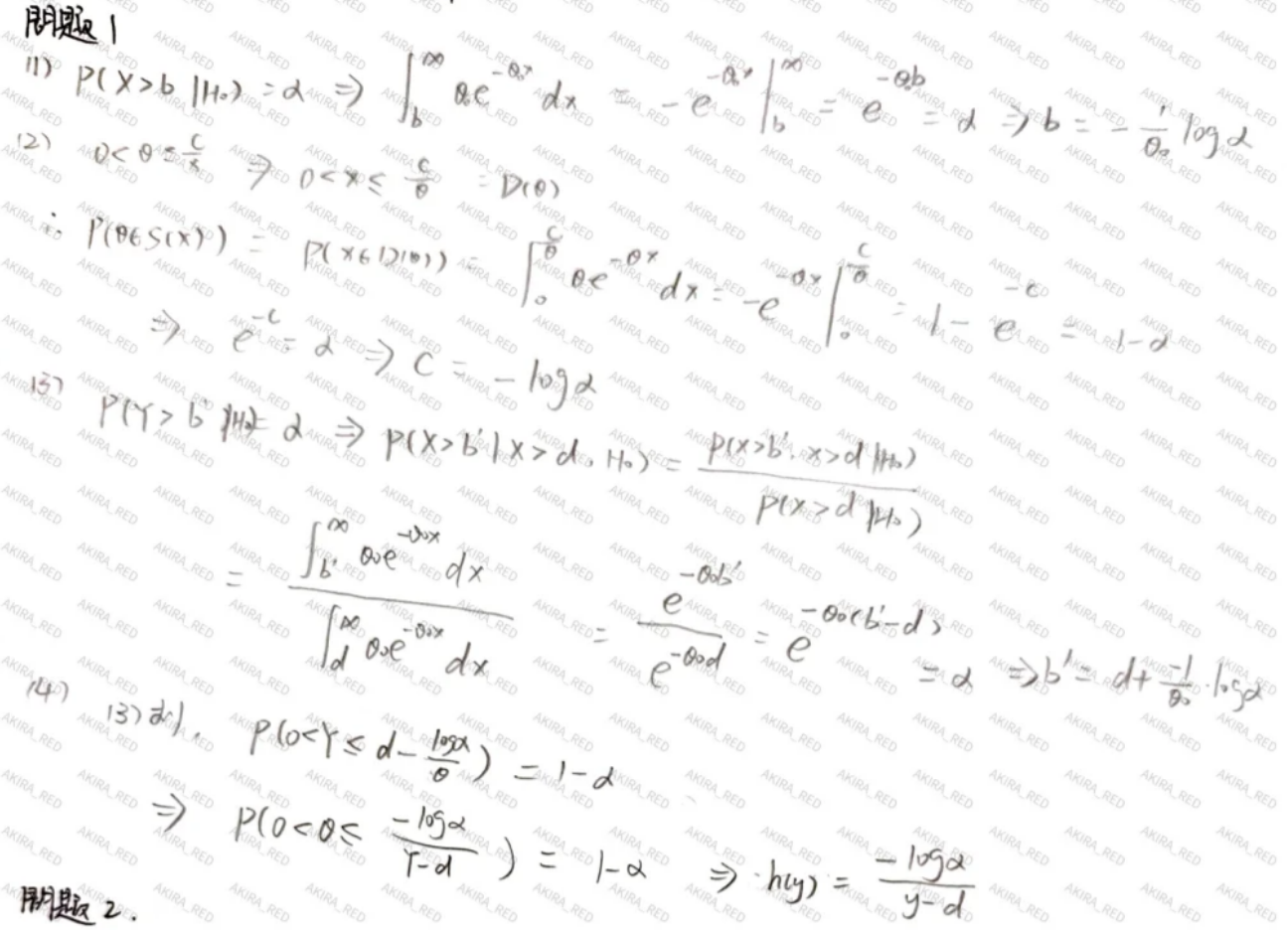京都大学 情報学研究科 システム科学専攻 2021年8月実施 専門科目 確率統計

标签：

• Kyoto-University
• Exponential-Distribution
• Hypothesis-Testing
• Confidence-Interval
• Cauchy-Distribution
• Gamma-Distribution
• Chi-Square-Distribution
• Moment-Generating-Function
• Method-of-Moments

Author

AKIRA (小红书:94184092292)

Description

問題1

確率変数 $X$ は確率密度関数

$$f(x; \theta) = \begin{cases} \theta e^{-\theta x}, & x > 0 \\ 0, & x \le 0 \end{cases}$$

の指数分布にしたがう。ただし $\theta > 0$ はパラメータである。 ある定数 $\theta_0 > 0$ に対して、帰無仮説 $H_0 : \theta = \theta_0$、対立仮説 $H_1 : \theta < \theta_0$ の仮説検定を有意水準 $\alpha \ (0 < \alpha < 1)$ で行いたい。 以下の設問に答えなさい。その導出過程も示すこと。

(1) 定数 $b > 0$ を定めておき、$X > b$ のとき $H_0$ を棄却する。 この仮説検定の有意水準が $\alpha$ となるような定数 $b$ を求めよ。

(2) 定数 $c > 0$ を定めておき、パラメータ $\theta$ の信頼区間を

$$S(x) = \left\{ \theta \mid 0 < \theta \le \frac{c}{x} \right\}$$

とする。$P(\theta \in S(X)) = 1 - \alpha$ を満たすような定数 $c$ を求めよ。

(3) 与えられた定数 $d > 0$ に対して、事象 $\{ X > d \}$ を条件とする $X$ の条件付き分布にしたがう確率変数 $Y$ を定義する。 すなわち、任意の $y > d$ に対して $P(Y > y) = P(X > y \mid X > d)$ である。 定数 $b' > d$ を定めておき、$Y > b'$ のとき $H_0$ を棄却する。この仮説検定の有意水準が $\alpha$ となるような定数 $b'$ を求めよ。

(4) 設問(3)の確率変数 $Y$ からパラメータ $\theta$ の信頼区間をつくりたい。 ある関数 $h(y)$ を用いて、

$$T(y) = \{ \theta \mid 0 < \theta \le h(y) \}$$

とする。$P(\theta \in T(Y)) = 1 - \alpha$ を満たすような関数 $h(y)$ を求めよ。

問題2

以下の設問に答えなさい。 ただし、$N(\mu, \sigma^2)$ は平均 $\mu$、分散 $\sigma^2$ の正規分布、$E[\cdot]$ は期待値を表す。

(1) 独立ではないが無相関であるような実確率変数の組 $(X, Y)$ の例を1つ挙げよ。 またそれが独立ではないこと、無相関であることの証明も示せ。

(2) $X$ と $Y$ を独立な $N(0, 1)$ に従う確率変数とする。 $Z = X / Y$ が従う確率分布の確率密度関数を求めよ。

以下の設問では、次のように定義される関数 $\Gamma(a)$

$$\Gamma(a) = \int_0^\infty x^{a-1} e^{-x} dx$$

および $a, b > 0$ なるパラメータを持つ確率密度関数 $g(x; a, b)$

$$g(x; a, b) = \begin{cases} (b^a \Gamma(a))^{-1} x^{a-1} e^{-\frac{x}{b}}, &x > 0 \\ 0, &x \le 0 \end{cases}$$

を用いる。 確率密度関数 $g(x; a, b)$ を持つ確率分布を $G(a, b)$ とする。 また必要であれば $a > 0$ に対して $\Gamma(a+1) = a\Gamma(a)$ を用いてよい。

(3) $G(a, b)$ に従う確率変数 $X$ について、そのモーメント母関数

$$M_X(r) = E[e^{rX}]$$

が有限であるような実数 $r$ の条件を示し、そのときの $M_X(r)$ の値を求めよ。

(4) 確率変数 $X_1, X_2, \ldots, X_n$ は独立で $N(0, v)$ に従うものとする。 このとき $Y = \sum_{i=1}^n X_i^2$ は、あるパラメータ $a_1, b_1$ を持つ $G(a_1, b_1)$ に従うことを示すとともに、$a_1, b_1$ を $v, n$ を用いて表せ。

(5) $G(a, b)$ に従う確率変数 $X$ の期待値 $\mu$ と分散 $\sigma^2$ を $a, b$ を用いて表せ。

(6) $x_1, x_2, \ldots, x_n$ をパラメータ $a, b$ が未知である $G(a, b)$ からの無作為標本とする。 設問(5)の結果とモーメント法を用いて、$a, b$ に対する推定値 $\hat{a}, \hat{b}$ を標本平均

$$\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i, \quad s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2$$

の関数として表せ。ただしモーメント法とは、パラメータを $K$ 個持つ確率密度関数 $f(x; \theta_1, \theta_2, \ldots, \theta_K)$ のモーメント

$$m_k(\theta_1, \theta_2, \ldots, \theta_K) = \int_{-\infty}^\infty x^k f(x; \theta_1, \theta_2, \ldots, \theta_K) dx$$

を標本モーメント

$$\hat{m}_k = \frac{1}{n} \sum_{i=1}^n x_i^k$$

と等しいと置き、$\hat{m}_k = m_k(\theta_1, \theta_2, \ldots, \theta_K)$ $(k = 1, \ldots, K)$ なる $K$ 個の連立方程式を $\theta_1, \theta_2, \ldots, \theta_K$ について解くことで、推定値 $\theta_1, \theta_2, \ldots, \theta_K$ を得る方法である。

Kai

問題1

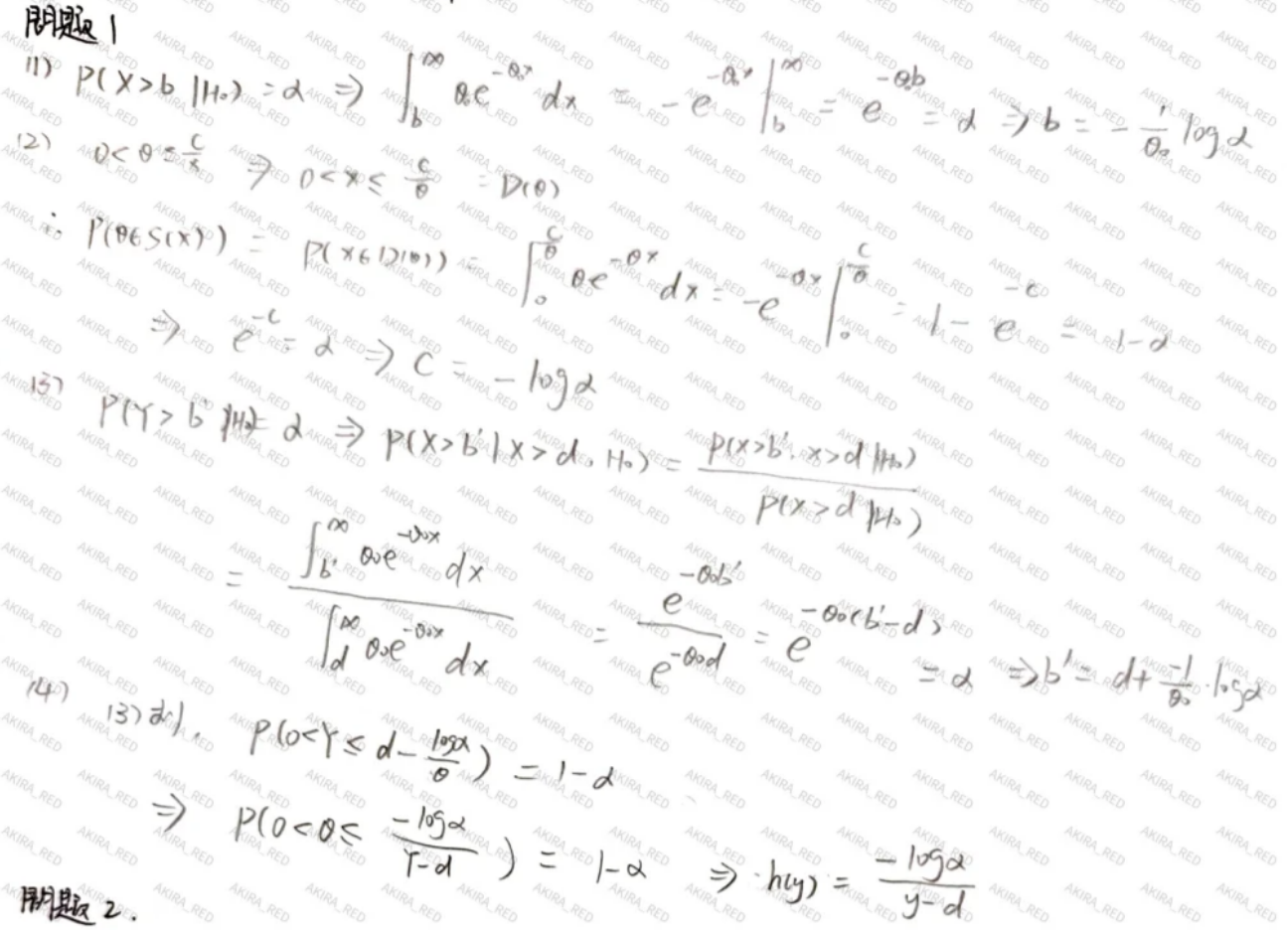
問題2