京都大学情報学研究科システム科学専攻 2021年8月実施数学【II】

Author

を実数全体からなる集合とし、をネイピア数（自然対数の底）とする。実数に対して -平面上の領域を

とし、以下の積分を考える。ただしは実数とする。

この積分を求めるために、以下の写像によって変数をに変換することを考える。

以下の設問に答えよ。なお、以降では自然数について次式が成り立つことを用いて良い。

(i) 上記の写像による領域の -平面上の像を求めよ。

(ii) 以下の空欄に入る式をを用いて表せ。

(iii) の値を求めよ。

(iv) 任意のに対して

が成立つことを示せ。

を直交座標系とする3次元ユークリッド空間における2つの楕円体

を考える。ただし、は正の定数とする。以下の設問に答えよ。

(i) 上の点におけるの接平面の方程式を求めよ。

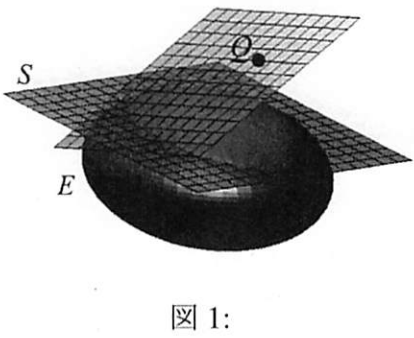
(ii) の外部の点を考える。を通るの接平面すべてを考え、それらの接点の集合をとする。は、ある平面に含まれる（図1）。平面の方程式を求めよ。

設問(ii)で求めたによるの切断面は楕円となる。以下ではこの楕円をとする。

(iii) 設問(ii)の点が楕円体上にあるとき、の中心座標を求めよ。

(iv) 設問(ii)の点が楕円体上を動くとき、設問(iii)で示したの中心座標について、各成分の積

が最大となる点とそのときのの値を求めよ。