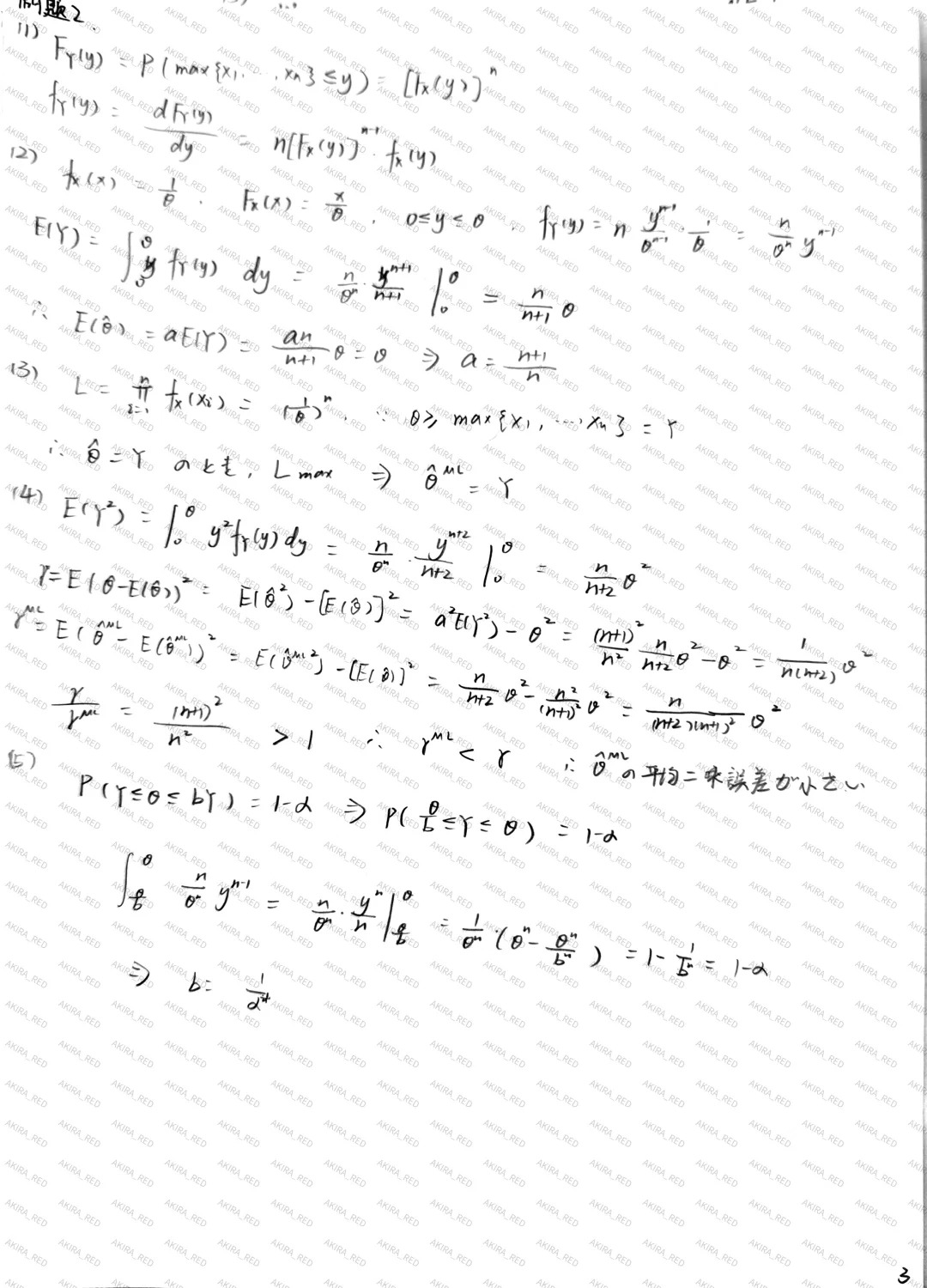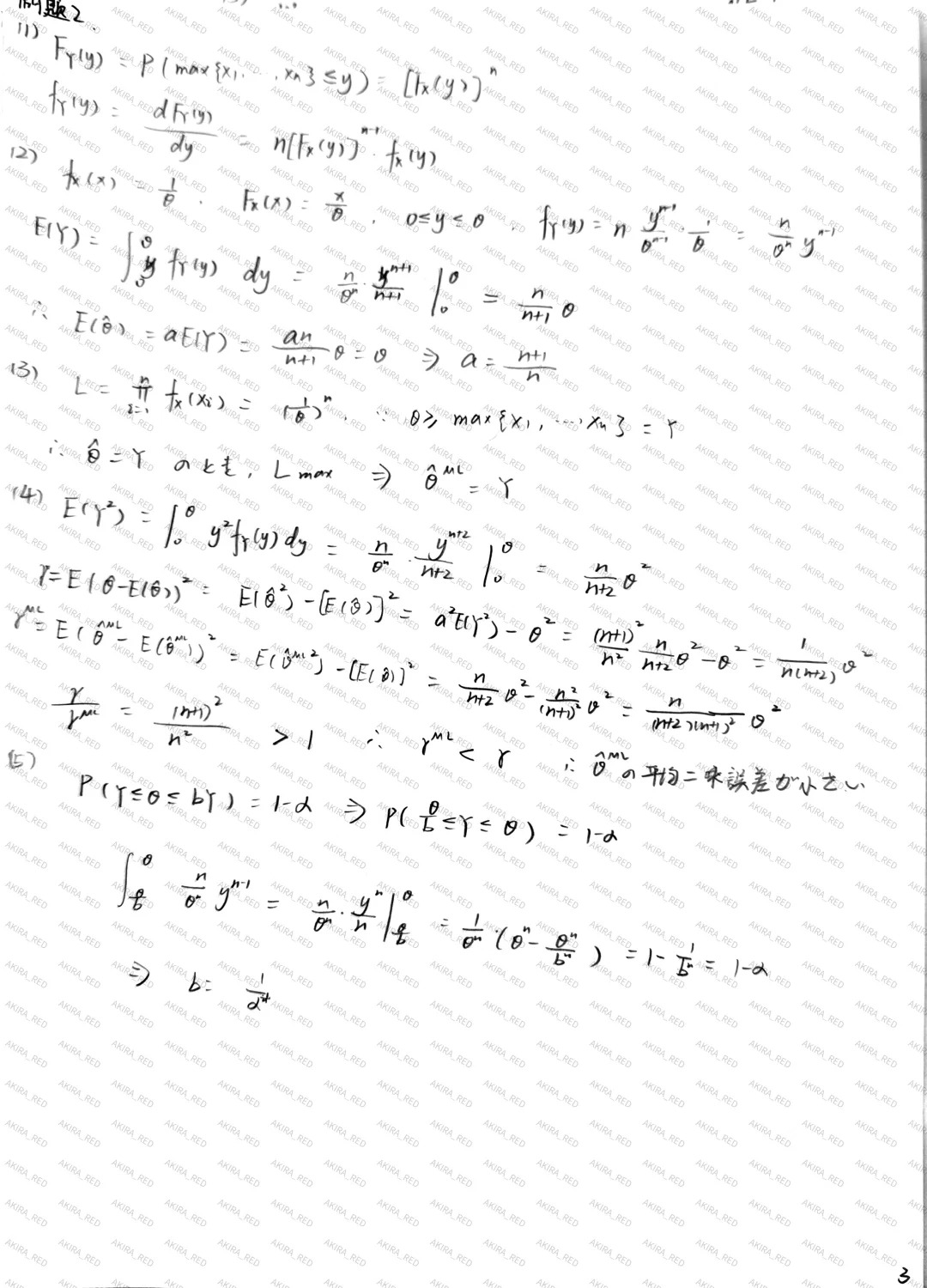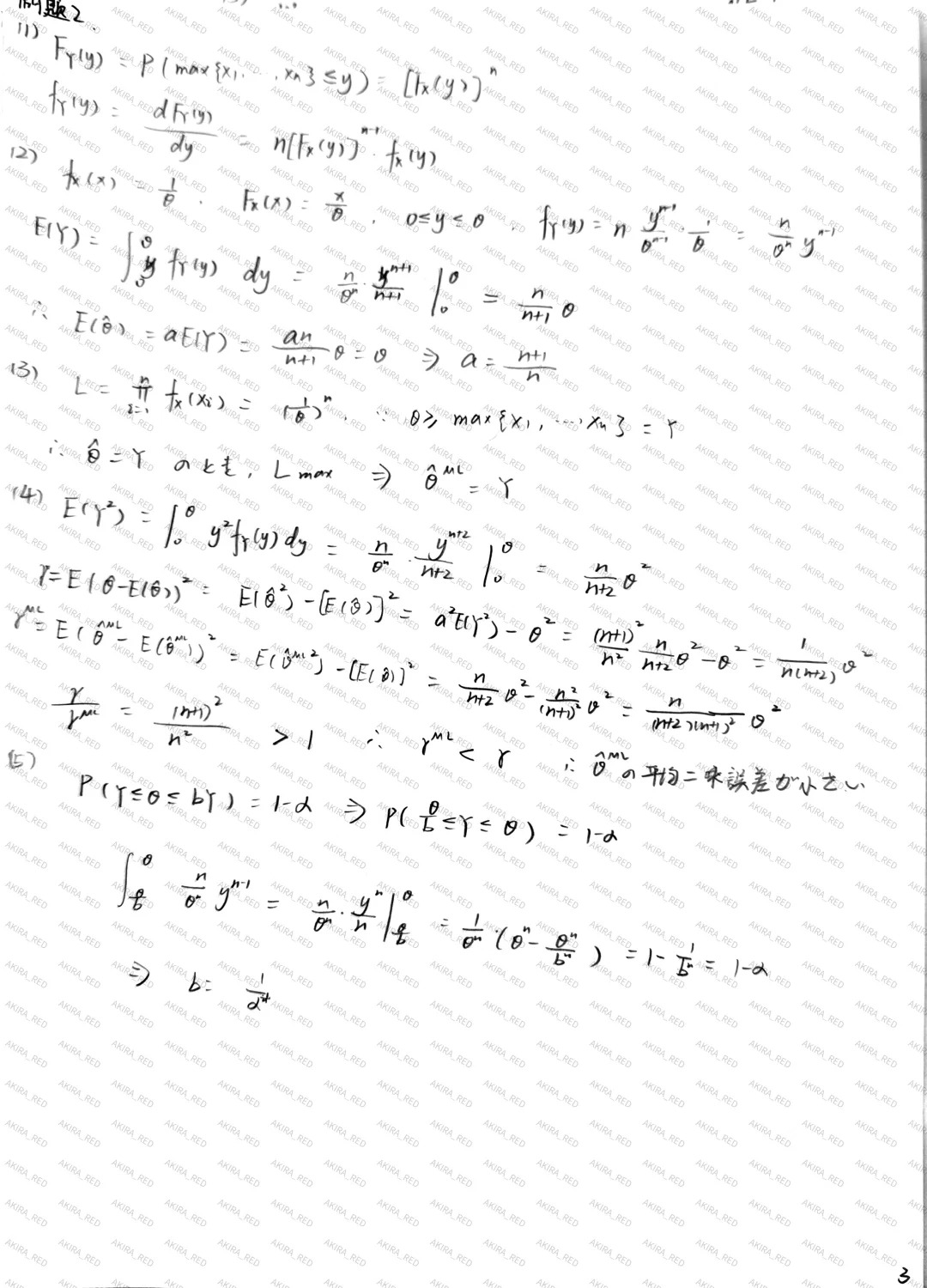京都大学情報学研究科システム科学専攻 2020年8月実施専門科目確率統計

Author

確率変数は独立に正規分布に従い、とする。ただし、は平均、分散の正規分布を表す。ここでは正の整数、は未知パラメータである。また、の分布関数で表す。以下の設問に答えなさい。その導出過程も示すこと。

(1) をすべて用いての最尤推定量を求めよ。

(2) がの不偏推定量であることを示せ。

(3) 各において、帰無仮説、対立仮説の仮説検定を有意水準で行いたい。そのために定数を定めておき、のとき帰無仮説を棄却する。定数を求めよ。

(4) 各において、ある定数を用いての信頼区間

を定める。これがを満たすようにしたい。定数を求めよ。

(5) 上記のが

を満たすようにしたい。として、定数を求めよ。

を互いに独立で、同一の確率密度関数に従う実数値確率変数とし、対応する確率密度関数・確率分布関数をそれぞれとする。また、

とする。以下の設問に答えなさい。

(1) の確率分布関数および確率密度関数をを用いて表せ。

以下の設問では、は区間上の一様分布に従うものとする。

(2) がの不偏推定量となるように、をを用いて表せ。

(3) の最尤推定量を求めよ。

(4) およびの平均二乗誤差を求め、どちらの推定量のほうが小さい平均二乗誤差を与えるか答えよ。ただし、は (2) で求めた不偏推定量である。

(5) の信頼区間として

の形を考える。に対して、となるようにを設定せよ。