跳到主要内容

京都大学 情報学研究科 通信情報システム専攻 2020年8月実施 専門基礎A [A-6]

Author​

祭音Myyura (with GPT-5)

Description​

(1)​

For manipulating a linear list structure of integer numbers in the main memory of a computer, let us consider the two implementation methods: an array structure, and one-way linked list using pointers. For the two methods, answer the number of computation steps required for executing the following operations in -notation. Let be the length of the list.

  • INSERT(x, p): Insert an element x at just after the cell located by the pointer p.
  • DELETE(p): Delete an element (if exists) at the next cell of the cell located by the pointer p.
  • FIND(i): Return the value of the i-th cell from the head.
  • NEXT(p): Return the location of the next cell of the cell located by the pointer p. (Return null if not exist.)
  • PREVIOUS(p): Return the location of the previous cell of the cell located by the pointer p. (Return null if not exist.)

(2)​

Answer the following questions on the procedure "something" shown by the following pseudo code.

something(int a, int b) {
  if (b == 0) return a;
  int r = a;
  while (r >= b) r = r - b;
  return something(b, r);
}

(a) Answer the return value of this procedure for the given arguments a = 12 and b = 15.

(b) What is calculated by this procedure if a pair of positive integers is input? Answer the arithmetic relation between the input and the output.

(c) Explain the behavior of this procedure if at least one of the input integers is less than or equal to zero.

(3)​

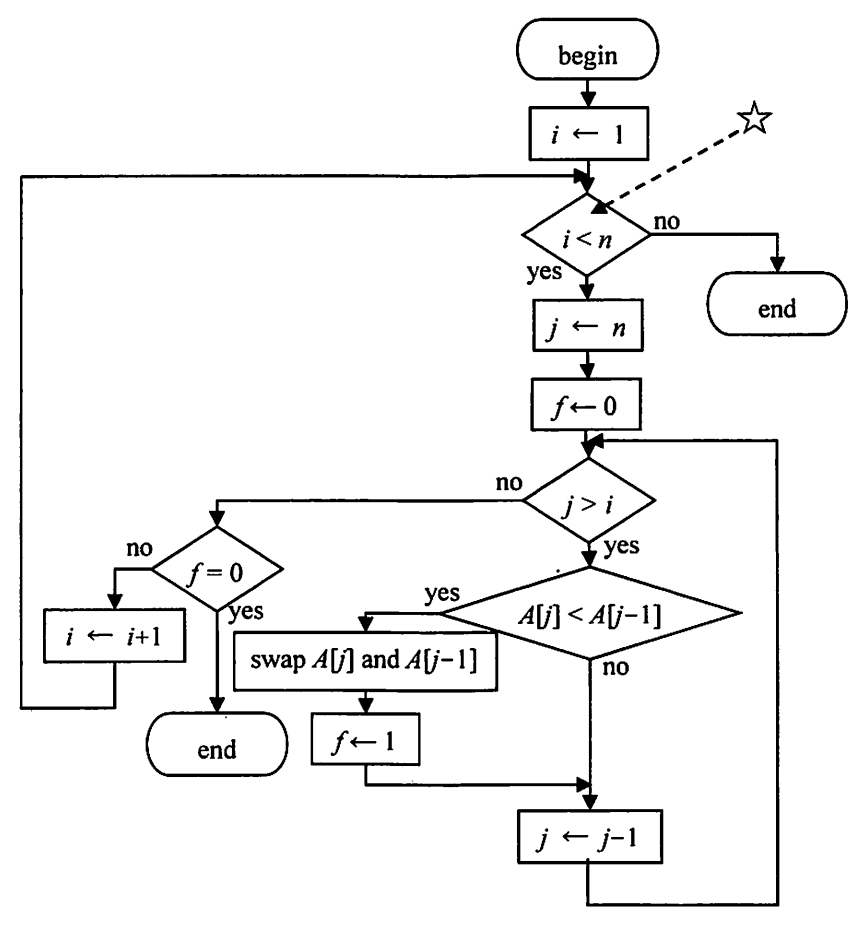
The following flowchart represents analgorithm manipulating a given array , each of which stores a numerical data. Answer the following questions.

(a) Explain how the contents ofthe array will be changed eventually by this algorithm.

(b) When , how many times will the ✩-marked block be visited at most?

(c) When n = 6 and the initial values of are , then how will the values of be changed on each visit of the✩-marked block during execution? List up those values on each visit.

(4)​

Describe the basic procedure of an algorithm for sorting a sequence of numerical data using merge sort. Then, explain its time complexity using n as the length of the sequence.

Kai​

(1)​

OperationArraySingly linked list
INSERT(x, p) (insert after cell p)shift tail → O(n)pointer splicing → O(1)
DELETE(p) (delete the next cell of p)shift tail → O(n)fix p->next and free → O(1)
FIND(i) (value of the i-th cell from head)random access → O(1)walk from head → O(i) (worst O(n))
NEXT(p)index+1 or bounds check → O(1)return p->next → O(1)
PREVIOUS(p)index−1 or bounds check → O(1)must scan from head to find the predecessor of p → O(n)

(2)​

(a)​

(b)​

For given positive integers a and b, it implements the Euclidean algorithm (using repeated subtraction / remainder). Output = gcd(a, b), the greatest common divisor.

(c)​

If at least one input is ≤ 0:

If b == 0, it returns a immediately (which might be ≤ 0).

If b < 0, the condition r >= b is always true and r = r - b increases r, so the loop does not terminate (infinite loop).

If a ≤ 0 and b > 0, the first call reduces to something(b, a); then a becomes non-positive as the second parameter, leading to the b == 0 base case (if a==0) or the non-terminating b < 0 case (if a<0).

(3)​

(a)​

Behavior: Each outer pass sets j ← n and scans left, swapping whenever A[j] < A[j-1]. That “bubbles” the smallest element of the unsorted suffix to position i. With the early-stop flag f, the algorithm eventually sorts the array in non-decreasing (ascending) order.

(b)​

With (n=10): the starred decision (“check i < n”) is visited once per outer pass, plus a final time when i == n. With no early stop, that is 10 visits (for i=1..9 true, then once more false).

(c)​

With (n=6) and initial :

  • 1st visit of ☆: array is [4,1,7,5,8,9] (start of pass). After the pass the smallest element is moved to the front → array becomes [1,4,5,7,8,9], f=1.
  • 2nd visit of ☆: array is [1,4,5,7,8,9]. No swap occurs (f=0) → terminate.

So the sequence observed at each ☆-visit is: [4,1,7,5,8,9] → [1,4,5,7,8,9].

(4)​

Procedure (top-down):

  1. If the sequence has size 0 or 1, it is already sorted.
  2. Split the sequence into two halves.
  3. Recursively sort the left half and the right half.
  4. Merge the two sorted halves by linear scanning with two pointers into a new array, then copy back (or write into an auxiliary array).

Complexities:

  • Time: each level merges elements, and there are levels → .
  • Space: requires auxiliary space (in-place variants are possible but non-trivial).
  • Stable: Yes (if implemented with stable merge).
目录