広島大学 先進理工系科学研究科 物理学プログラム 2022年8月実施 専門科目 [1] 力学
Author
Miyake
Description
ばね定数 のばねが、滑らかで水平な床に置かれ、片側は壁に固定されており、もう片方に質量 の質点が取り付けられている。
空気から質点には速度に比例した抵抗が働くものとし、その比例係数を とする。
ばねは平行に座標 を取り、ばねが自然長の時の質点の位置を原点とし、壁と逆側の向きを正の方向とする。壁に垂直な方向の質点の運動のみ考えることとして、以下の問いに答えよ。
(1) この系の運動方程式を立てよ。
(2) のとき、運動方程式の一般解を求め、どのような運動をするのか図を用いて説明せよ。
(2) のとき、運動方程式の一般解を求め、どのような運動をするのか図を用いて説明せよ。
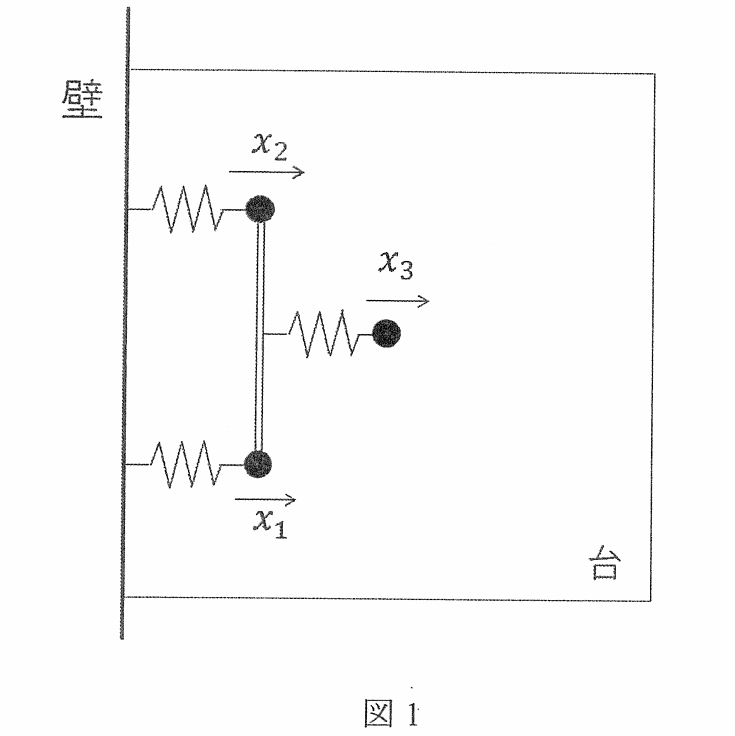
図 1 のように３つの質点と３つのばねと1つの棒が組み合わされて構成され、壁に取り付けられて水平な台に置かれた系を考える。
すべての質点の質量を 、すべてのばねのばね定数を とする。
また、棒の長さを とし、1つのばねは棒の中点の場所に取り付けられているものとする。
棒は伸び縮みせず、たわまないものとし、棒の質量は無視できるものとする。
台の表面は滑らかであるとする。
それぞれの質点の座標を とし、ばねが自然長の時の質点の位置を原点とし、壁と逆側の向きを正の方向とする。
この系の質点の振動モードについて以下の問いに答えよ。
ただし、質点の振動の振幅は小さいものとし、壁に垂直な運動のみ考えるものとし、壁に平行な方向の運動は微小なものとして無視する。
空気からの抵抗も考えない（）ものとする。
(1) この系のラグランジアンを求めよ。
(2) 上で求めたラグランジアンより、この系の運動方程式を導出せよ。
(3) この系の固有振動モードの1つは、棒の中点が静止した状態で、棒の両端が逆位相で振動するものである。
棒の中点の周りに関する回転の運動方程式を導出し、その角振動数が であることを示せ。
上の (2) で求めた式を利用しても良い。
(4) この系の固有角振動数について、 以外の2つを求めよ。
(5) この系の固有振動モードは3種類ある。それぞれを図を用いて説明せよ。
Kai
時刻を で表し、時間微分を や で表す。
(1)
(2)
(1) の運動方程式に （ は によらない定数）を代入すると、
を得る。よって、 のときの一般解は、任意定数を として、
である。
(3)
のときの一般解は、任意定数を として、
である。
(1)
求めるラグランジアン は、
(2)
より、
(3)
(2) で求めた運動方程式は、次のように書ける：
の場合を考えると、
となるので、これは角振動数 の固有振動モードであることがわかる。
(4)
(3) で現れた行列
の固有値を とすると、
なので、 以外の固有角振動数は である。
(5)
(4) の行列 の固有値 に属する固有ベクトルはそれぞれ
であるので、固有角振動数 の固有振動モードはそれぞれ
と書ける。（ は初期条件から決まる定数である。）