広島大学 先進理工系科学研究科 情報科学プログラム 2022年1月実施 専門科目II 問題2

Author

祭音Myyura

Description

以下の問いに答えよ。

(1) Table 1 は鳥取 (Tr)、島根 (S)、岡山 (O)、広島 (H)、山口 (Y)、徳島 (Tk)、愛媛 (E) の7つの各都市間の距離を表す。 都市を頂点とし、距離を都市間の辺の重みとしたグラフ の最小全域木を求めよ。

(2) 各辺の重みがすべて異なる任意のサイズの重み付き連結グラフ において、最小全域木を求めるアルゴリズムを説明せよ。

(3) (2) で述べたアルゴリズムで求められる部分グラフが最小全域木であることを証明せよ。

(4) (2) で述べたアルゴリズムの計算時間複雑性を理由とともに示せ。

(5) 重み付き連結グラフ において、各辺の重みがすべて異なっている時、 は唯一の最小全域木を持つことを証明せよ。

---

Answer the following questions

(1) Table 1 shows the distances between the seven cities of Tottori (Tr), Shimane (S), Okayama (O), Hiroshima (H), Yamaguchi (Y), Tokushima (Tk), and Ehime (E): Find the minimum spanning tree of graph with the cities as nodes and the distances as weights of the edges between the cities.

(2) Describe an algorithm to find the minimum spanning tree in a weighted connected graph of any size where all edges have distinct weights.

(3) Prove that the subgraph obtained by the algorithm described in (2) is the minimum spanning tree.

(4) Show the time complexity of the algorithm described in (2) with reasons.

(5) In a weighted connected graph , prove that has a unique minimum spanning tree when all edges have distinct weights.

Table 1

	Tr	S	O	H	Y	Tk	E
Tr	-	108	97	204	292	162	229
S	108	-	121	131	203	298	183
O	97	121	-	139	233	88	141
H	204	131	139	-	94	197	78
Y	292	203	233	94	-	258	126
Tk	162	298	88	197	258	-	168
E	229	183	141	78	126	168	-

Kai

(1)

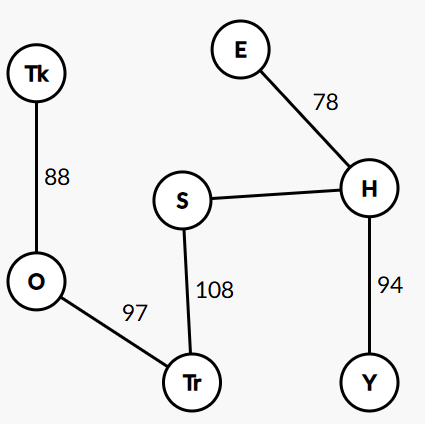
(2)

(Prim's algorithm)

Step 1: Determine an arbitrary vertex as the starting vertex of the MST.

Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST (known as fringe vertex).

Step 3: Find edges connecting any tree vertex with the fringe vertices.

Step 4: Find the minimum among these edges.

Step 5: Add the chosen edge to the MST if it does not form any cycle.

Step 6: Return the MST and exit

(3)

Let , , denote the vertex set, the edge set and edge weights of .

It is trivial that the subgraph obtained by Prim's algorithm is a tree. Let denote the subgraph.

Let denote a minimum spanning tree of graph . If , then is a minimum spanning tree. Otherwise, let be the first edge added during the construction of tree that is not in tree , and be the set of vertices connected by the edges added before edge . Then one endpoint of is in set and the other is not. Since is connected, there exists an edge such that one endpoint of is in set and the other is not. Hence at the iteration when edge was added to , edge is also one of alternatives. Since edge was not chosen, we know that

Let . Since , is also a minimum spanning tree which contains edge and all the edges added before it during the construction of set . Repeat the steps above and we will eventually obtain a minimum spanning tree of graph that is identical to tree , which shows that is a minimum spanning tree.

(4)

If we use an adjacent list graph representation and a binary heap to find an edge of minimum weight, then the worst-case time complexity is

(5)

Assume the contrary, that there are two different MSTs and .

Since , there is at least one edge that belongs to one but not the other. Among such edges, let be the one with least weight; this choice is unique because the edge weights are all distinct. W.l.o.g, assume .

As is an MST, must contain a cycle with . As a tree, contains no cycles, therefore must have an edge that is not in . Since was chosen as the unique lowest-weight edge among those belonging to exactly one of and , the weight of must be greater than the weight of . As and are part of the cycle , replacing with in therefore yields a spanning tree with a smaller weight, which contradicts the assumption that is an MST.