広島大学 先進理工系科学研究科 情報科学プログラム 2019年8月実施 専門科目II 問題2

Author

samparker, 祭音Myyura

Description

子の数に制約のない根付き木を 分木によって表す方法として、左子・右兄弟表現がある。 2 分木の各節点 は、キー の他に、親 と左端の子 、すぐ右の兄弟 の３つのポインタを持つ。 親や左端の子、すぐ右の兄弟がいない節点では、それぞれのポインタ の値は とする。 例えば、図 1 (a) の根付き木を上述の表現の二分木で表すと図 1 (b) のようになる。

(1) 根付き木の節点の数を 、枝の数を とする。 と の関係を書け。

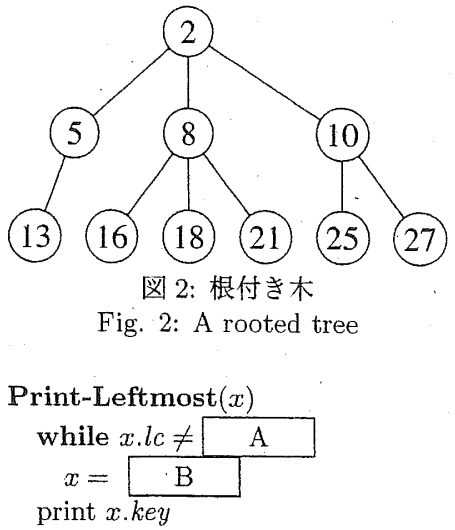
(2) 図 2 の根付き木を、左子・右兄弟表現の 2 分木で表せ。ポインタ は省略せよ。

(3) 根付き木の根 が与えられたとき、一番左下の子孫の を出力する手続きの擬似コード Print-Leftmost() を示す。空欄 と を適切に埋めよ。

(4) 根付き木の根 が与えられたとき、すべての節点の を出力する手続き Tree-Walk() を擬似コードで書け。ただし、節点を出力する順序は問わない。

(5) (4) の手続き Tree-Walk() の時間計算量をオーダー表記で書け。

---

There is the left-child, right-sibling representation that uses a binary tree to represent a rooted tree with arbitrary number of children. Each vertex of the binary tree contains a key , a parent pointer , a pointer to the leftmost child , and a pointer to the sibling immediately to its right . We assume that, in case of no parent, no child, or no sibling, the value of the pointer or is null, respectively. For example, a rooted tree shown in Fig. 1 (a) is represented by a binary tree of the above representation as shown in Fig. 1 (b).

(1) We assume that a rooted tree has vertices and edges. Describe the relationship between and .

(2) Draw a binary tree of the left-child, right-sibling representation, to represent a rooted tree shown in Fig. 2. The pointer should not be drawn.

(3) The pseudo code Print-Leftmost() is a procedure that prints the key of the leftmost descendant of a tree rooted at a given node . Fill the blanks and .

(4) Write a pseudo code of the procedure Tree-Walk() that prints keys of all vertices in a tree rooted at a given node . The order of vertices to print is not the matter.

(5) Show the execution time of Tree-Walk() using big-O notation.

Kai

(1)

(2)

                            2
                        /
                       5
                   /       \
                  13        8
                        /       \
                       16       10
                         \    /
                         18  25
                           \   \
                           21  27

(3)

(4)

Tree-Walk(x)
    if (x != null) then
        print(x.key)
        Tree-Walk(x.lc)
        Tree-Walk(x.rs)

(5)