東京工業大学 工学院 電気電子系 2023年8月実施 電磁気学2

Author

Zero, 祭音Myyura

Description

コイルに関する以下の問に答えよ。特に指定がない限り，各設問は真空中での実験とし，必要に応じて真空透磁率 を用いてもよい。

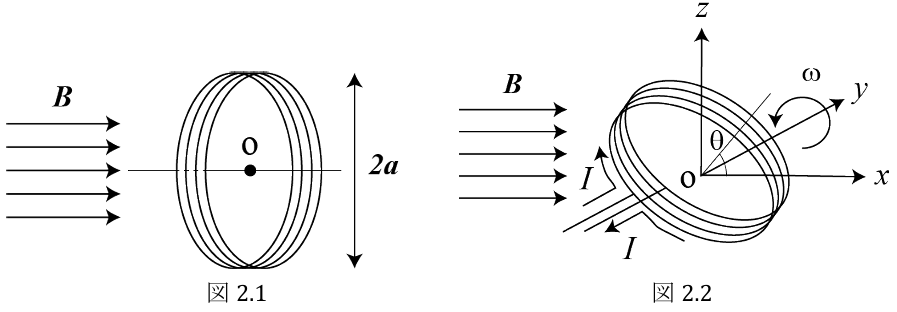
(1) 図 のように半径 , 巻数 , 抵抗値 , 両端が短絡されている円形コイルがある。次の問に答えよ。

• ① このコイルが磁束密度 の一様かつ一定な磁場がかかる場所においてあるとき，コイル内に生じている起電力および電流を求めよ。磁束密度の方向と円形コイルの中心軸方向は一致している。なお，電流によって発生する磁束密度は，磁束密度 に比べて十分小さいため無視できるものとする。

• ② 前問において，磁束密度を時間 , 角周波数 を用いて で変化させたとき，コイル内に生じる起電力および電流を求めよ。

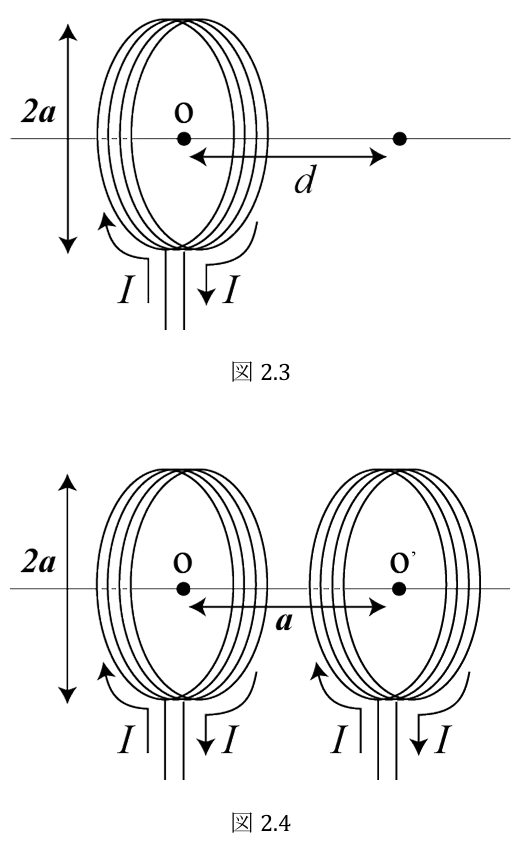
(2) 図 のように半径 , 巻数 , 抵抗値 の円形コイルが，磁束密度 の一様かつ一定な磁場がかかる場所にあり，磁束密度 ( 軸方向) に直交する 軸の周りに角速度 で回転している (コイルの中心軸は 平面内で回転している)。磁束密度の方向とコイルの中心軸とのなす角度を とする。時刻 のとき，磁束密度の方向とコイルの中心軸の方向は一致している 。次の問に答えよ。なお，電流によって発生する磁束密度は，磁束密度 に比べて十分小さいため無視できるものとする。

• ① コイル内に生じる起電力および電流を求めよ。ただし，コイルの両端は短絡されているものとする。

• ② 前問において， が任意の つの角度 から まで ( ただし， ) 変化する間に，巻線内を移動した電荷量 と角速度 の間の関係を理由とともに答えよ。

• ③ このコイルに電流 を流した。ある角度 におけるトルクを求めよ。

(3) 図 のように半径 , 巻数 の円形コイルを，外部磁場が存在しない場所に置き，電流 を流してしばらく待った。

• ① 円形コイルの中心 から中心軸上を距離 離れた点における磁束密度の大きさを求めよ。

• ② 図 のように，図 の中心軸上に 離れた点 を中心として，同じ円形コイルを設置し，同じ向きで電流 を流してしばらく待った。この時に，コイル間の中心軸上の 点 間の中点における磁束密度の大きさを求めよ。また，このようなコイル配置では，コイル間中心軸上の磁束密度は，どのような特徴をもつか。

Kai

(1)

①

で が一定より、起電力 、電流 。

②

• 起電力:
• 電流:

(2)

①

より、

よって、(1) - ② と同様にして、

• 起電力:
• 電流:

②

よって、電荷量 は、 に依存しない。

③

相互インダクタンスは、

エネルギー は

よって、トルク は

(3)

①

ビオ・サバールの法則と、対称性より、

②

①において、 とし、磁束密度の大きさを 倍する。

コイル間中心軸よで、一定、一様の磁束密度が表れる。