東京工業大学 工学院 電気電子系 2023年8月実施 電磁気学1

Author

Zero, 祭音Myyura

Description

半径 の円筒導体 の外側を，半径 の円筒導体 で囲った同軸線路が真空中にある。同軸線路の中心軸を 軸にとり， 軸からの距離を とする。円筒導体 と はともに完全導体であり，厚みを無視できるものとする。 導体間は，半径 の円筒面を境にして，内側は誘電率 , 外側は誘電率 の誘電体が充填されている。同軸線路の長さ は半径 に比べて十分長く，端部効果は無視できるものとする。真空の誘電率は , 誘電体の透磁率は真空の透磁率 と等しいものとして，以下の問に答えよ。

(1) 図 のように，電圧源，抵抗，スイッチ，配線を介して，円筒導体 と の 箇所の端部を繋げて閉回路を形成し，それぞれ電流の往路と復路の同軸線路と見なす。円筒導体 を 軸の負の向きに電流 が，円筒導体 を 軸の正の向きに電流 が，それぞれ一様に流れている。

• ① における磁界の大きさ を求めよ。
• ② における磁界の大きさ を求めよ。
• ③ 導体間において電流経路に鎖交する磁束 を求めよ。
• ④ この円筒導体 と からなる同軸線路の自己インダクタンス を求めよ。
• ⑤ この円筒導体 と からなる同軸線路が蓄えている磁気エネルギーを求めよ。同軸線路の自己インダクタンスとして を用いてよい。

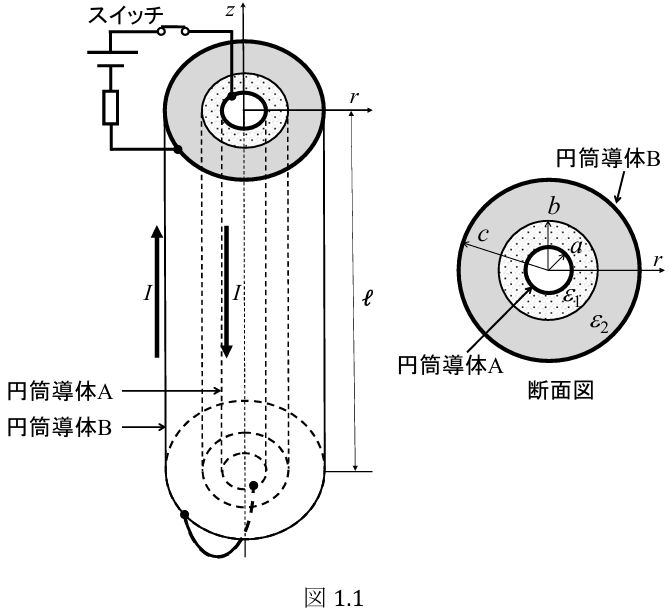
(2) 次に，図 のように，下端部の配線のみを変更し，円筒導体 を接地して十分に時間が経過したところ，円筒導体 に電荷 が帯電した。その後，図 のように，スイッチをオフにした。

• ① における電束密度 を求めよ。
• ② における電界の大きさ をそれぞれ求めよ。
• ③ における電界の大きさ を求めよ。
• ④ この円筒導体 と からなるコンデンサの静電容量 は以下の式で与えられる。

       空欄（ あ ）および（ い ）に入る数式をそれぞれ答えよ。

• ⑤ この円筒導体 と からなるコンデンサが蓄えている静電エネルギーを求めよ。コンデンサの静電容量として を用いてよい。

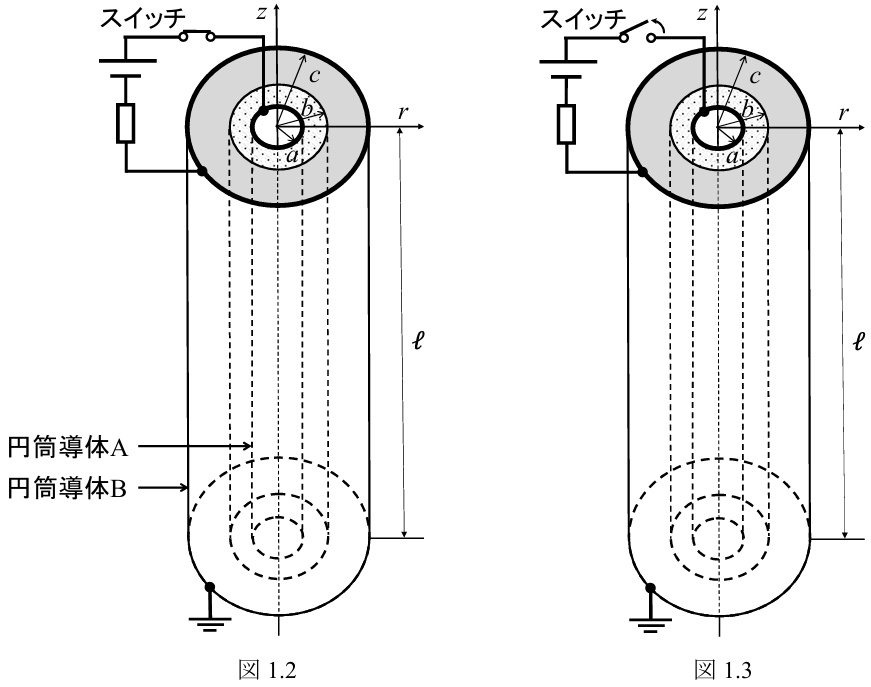
(3) さらに，図 のように，この円筒導体 の外側に導体球を離して置き，その導体球に電荷 を与えた。この後，十分に時間が経過したときの円筒導体 の電荷量を答えよ。

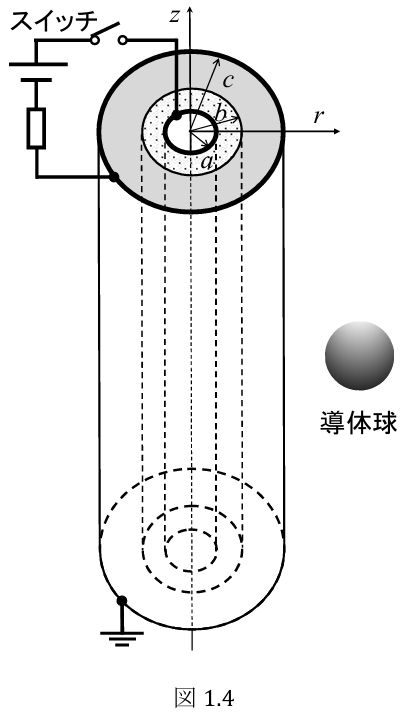
(4) 最後に，この円筒導体 と導体球を接触させて十分に時間が経過した後に，導体球を離した。さらに十分に時間が経過したときの円筒導体 の電荷量を答えよ。

Kai

(1)

①

アンペールの法則より、

②

等量異符号の電流が鎖交するので、

③

④

より、

⑤

(2)

①

ガウスの法則より、

②

(i)

(ii)

③

接地されているので、

④

間の電位差 は

従って、

⑤

(3)

静電遮蔽より、 の電荷量は である。

(4)

円筒導体 は、接地されているので、電荷量は である。