東京工業大学 工学院 電気電子系 2022年8月実施 電磁気学2

Author

Zero

Description

正の電荷 を持つ荷電粒子の真空中での運動について，以下の問に答えよ。荷電粒子の質量を とする。

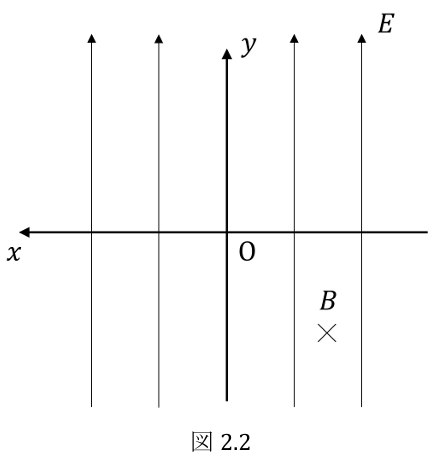
(1) 図 のような一様な磁束密度 の磁場および電場 の中での荷電粒子の運動を考える。領域 I では，磁場は紙面鉛直方向 (表面から裏面の方向) を向いており，電場は 方向を向いている。一方，領域 II では電場はなく，紙面鉛直方向 (表面から裏面の方向) の一様な磁束密度 の磁場のみがある。

の位置から荷電粒子を 方向に初速度 で入射させたとき，荷電粒子は領域 I 内を 方向に直進した。

① 荷電粒子が磁場および電場から受ける力の大きさと方向をそれぞれ求めよ。

② 荷電粒子が 方向に直進するための初速度 の条件を求めよ。

次に，荷電粒子が電場のない領域 II に飛び出した後の運動を考える。

③ 領域 II 内での荷電粒子の軌跡の概略図を描け。ただし，荷電粒子が領域 I と領域 II の境界に戻ってくるまでの軌跡でよい。

④ 領域 II に飛び出した荷電粒子が，領域 I と領域 II の境界に戻ってくるまでに到達する の最大値を としたとき, から までに外力が荷電粒子にする仕事を求めよ。

(2) 図 のような一様な磁束密度 の磁場および電場 の中での荷電粒子の運動を考える。磁場は紙面鉛直方向 (表面から裏面の方向) を向いており，電場は 方向を向いている。時刻 のときに，原点 に荷電粒子を静かにおいた。そのときの荷電粒子の初速度は である。

① 時刻 における荷電粒子の 方向と 方向の速度をそれぞれ とすると， 方向と 方向の運動方程式は式 (2.1) と式 (2.2) のように表される。空欄 および に入る数式を求めよ。

② 式 (2.1) および式 (2.2) から を消去することで, の微分方程式を求めよ。ただし， とし，答には を用いること。

③ は，それぞれ式 (2.3) と式 (2.4) で表される。空欄 に入る数式を求めよ。答には を用いること。

④ 荷電粒子が到達する の最大値 を求めよ。答には を用いること。

Kai

(1)

①

磁場: 軸正方向

電場: 軸負方向

②

力のつり合いより、

③

④

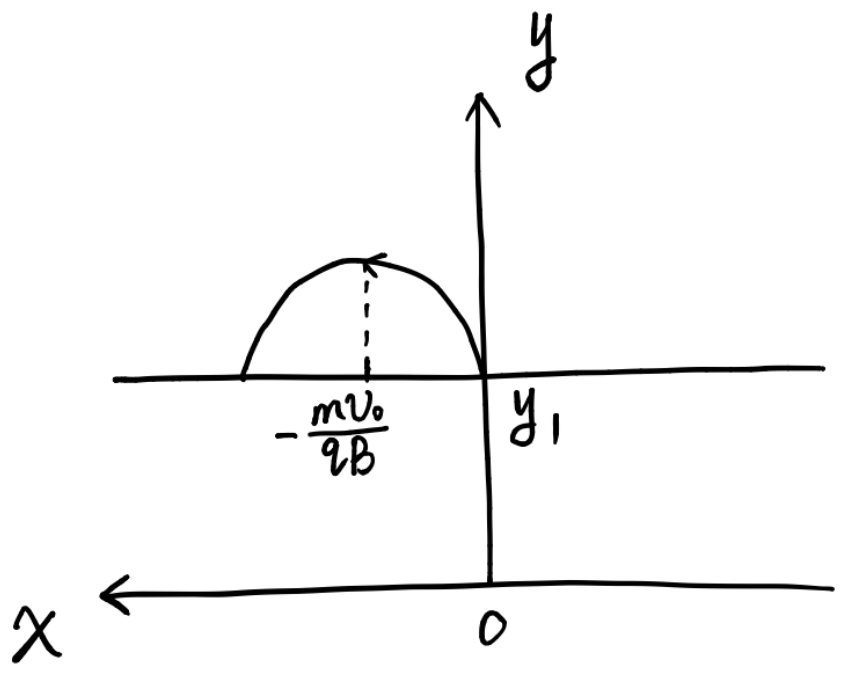
を中心とした、半径 の等速円運動を行うので、

また、円運動の中心方向に外力がカロれるので、進行方向との内積は より、外力の仕事は 。

(2)

①

②

(1) 式に代入、

③

(2) 式の特性方程式は、

従って、

④