東京工業大学 工学院 電気電子系 2021年8月実施 電磁気学2

Author

Zero

Description

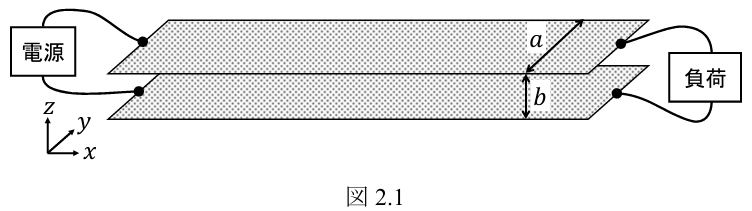
図 のような，真空中に 軸と平行に置かれた完全導体の平行平板線路について考える。平板の幅は , 平板の間隔は であり, である。平板の長さは 方向に十分長く,平板の厚さは十分薄い。線路の左端部に電源，右端部に負荷を接続した際の，平板間の空間における電磁界について以下の問に答えよ。線路における端部効果は無視する。また，真空の誘電率，透磁率をそれぞれ とする。

(1) 電源は直流電流源とし，負荷は短絡とすることで，上の導体に 下の導体に の電流を 方向に定常的に流した。以下の問に答えよ。ただし， 方向の電流分布は一様とする。

• (a) 平板間の空間における磁束密度の大きさを答えよ。また，磁束密度の向きは 軸のいずれと平行か答えよ。

• (b) 線路の単位長さあたりのインダクタンス を求めよ。

(2) 電源は直流電圧源とし，負荷は開放とすることで，上および下の導体に，それぞれ単位長さあたり電荷密度 の電荷が生じた。以下の問に答えよ。ただし， 方向の電荷分布は一様とする。

• (c) 平板間の空間における電界の大きさを答えよ。また，電界の向きは 軸のいずれと平行か答えよ。

• (d) 線路の単位長さあたりのキャパシタンス を求めよ。

(3) 電源は交流電流源とし，負荷は右端部で電流の反射が無いよう整合負荷とした。このとき，線路上の位置 , 時間 において，角周波数 で上の導体に , 下の導体に の交流電流が 方向に定常的に流れ，平板間の空間に平面波が 方向に伝搬する。以下の問に答えよ。ただし， 方向の電流分布は一様とし， は波数とする。また，(f) と (h) は導出過程も記せ。

• (e) 平板間の空間における磁束密度 を答えよ。

• (f) 電流連続の式より，上の導体の単位長さあたりの電荷密度 を求めよ。

• (g) (f) で求めた電荷密度 より，平板間の空間における電界 を答えよ。

• (h) (e) と (g) で求めた磁束密度 と電界 について，ファラデーの電磁誘導の法則の微分形を適用して， の間に成り立つ関係を導出し，平面波の位相速度を を用いて表せ。

Kai

(1)

(a)

アンペールの法則より、上下の平板が作る磁界は、

従って、

(b)

よって、 より、。

(2)

(c)

(d)

(3)

(e)

(f)

電流連続の式より、

(g)

(h)

従って、