東京工業大学 工学院 電気電子系 2021年8月実施 電磁気学1
根据中华人民共和国商务部公告2026年第12号,东京科学大学(東京科学大学/Institute of Science Tokyo)已被列入关注名单。请中国留学申请者慎重考虑相关风险,在做出留学决定前充分了解相关政策及其可能带来的影响。
Author
Zero
Description
完全導体からなる円筒状電極をもつ長さ
(1) 図
-
(a) 印加電圧
によって,内側および外側の円筒に,それぞれ単位長さあたり および の電荷が誘起されるとする。このとき,円筒の中心軸から垂直方向に距離 離れた点 における電界強度を求めよ。 -
(b) 点
における電位を求めよ。 -
(c)
つの円筒間の単位長さあたりのキャパシタンスを求めよ。
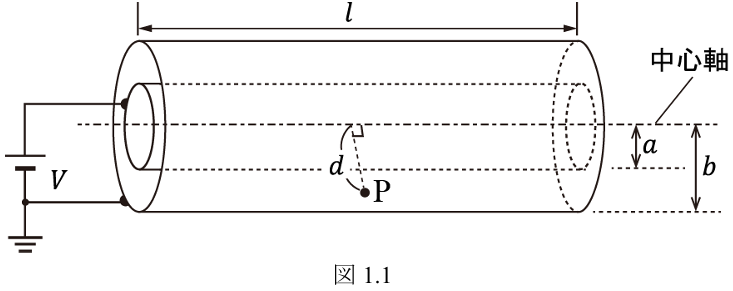
- (d) 図
のように,中心軸からの距離 とともに誘電率が変化する誘電体で つの円筒間を満たすと,電界が によらず一定となった。このとき,誘電率が距離 に対してどのように変化するか説明せよ。
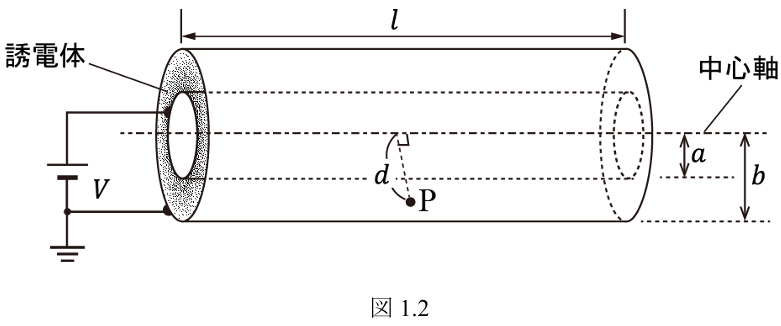
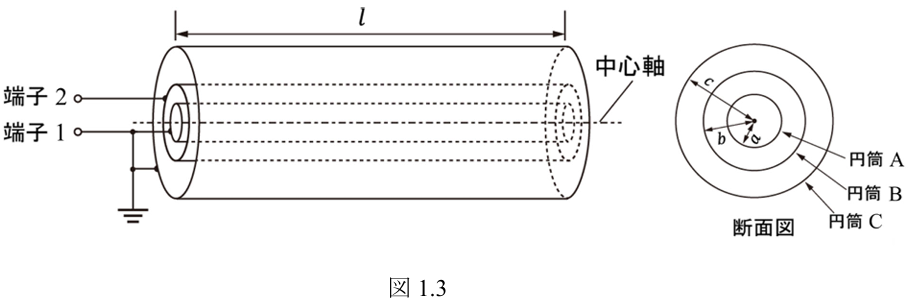
(2) 図
-
(e) 円筒
と円筒 につながる端子 と円筒 につながる端子 との間の単位長さあたりのキャパシタンスを求めよ。 -
(f) 円筒
に単位長さあたり の正電荷があるとき,円筒 と円筒 に誘起される単位長さあたりの電荷量を,それぞれ符号を含めて求めよ。
Kai
(1)
(a)
ガウスの法則より、
(b)
従って、
(c)
(d)
(2)
(e)
円筒
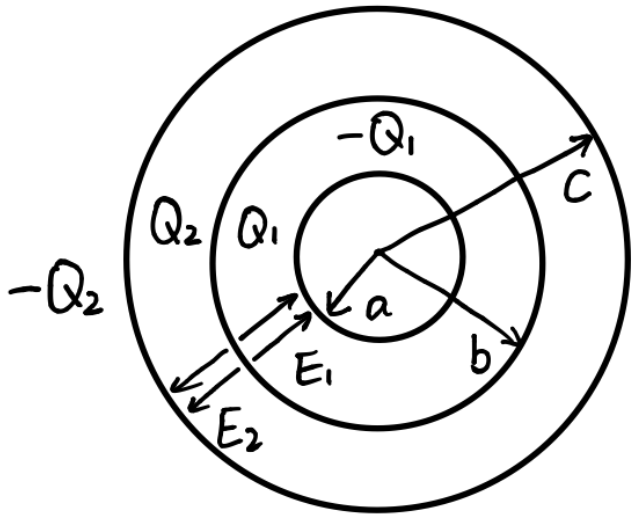
このとき、
また、
よって、