東京工業大学 工学院 電気電子系 2019年8月実施 電磁気学2
根据中华人民共和国商务部公告2026年第12号,东京科学大学(東京科学大学/Institute of Science Tokyo)已被列入关注名单。请中国留学申请者慎重考虑相关风险,在做出留学决定前充分了解相关政策及其可能带来的影响。
Author
Zero
Description
直流電流の作る磁界に関する,以下の設問 (1) および (2)に答えよ。
(1)
「図 2.1 のように円電流の微小線素ベクトル
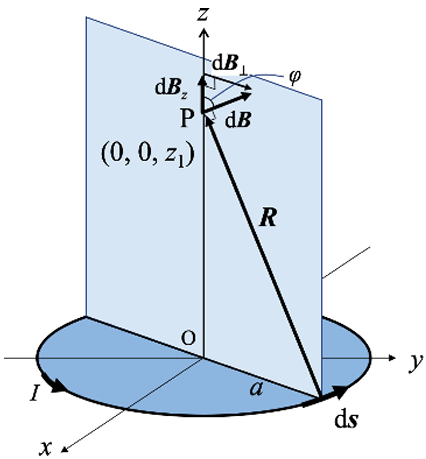
(2) 図
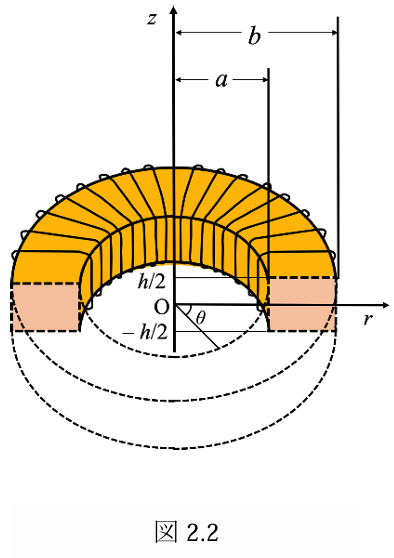
- (a) コアの内側
では,図 のような円柱座標系 を用いると,コイルに流れる直流電流 による磁界が
となることを示せ。
-
(b) コアの外側では,コイルに流れる直流電流
による磁界がゼロとなることを説明せよ。 -
(c) コアの断面
を貫く磁束 は,次式で表されることを示せ。ただし, は の自然対数を表す。
-
(d) 環状コイル全体に蓄えられた磁界のエネルギー
を求めよ。 -
(e) この環状コイルの自己インダクタンス
を求めよ。
Kai
(1)
① 0
② ビオ・サバールの法則より、
③
④
⑤
⑥
(2)
(a)
アンペールの法則より、積分路を円周上にすると、
(b)
積分路
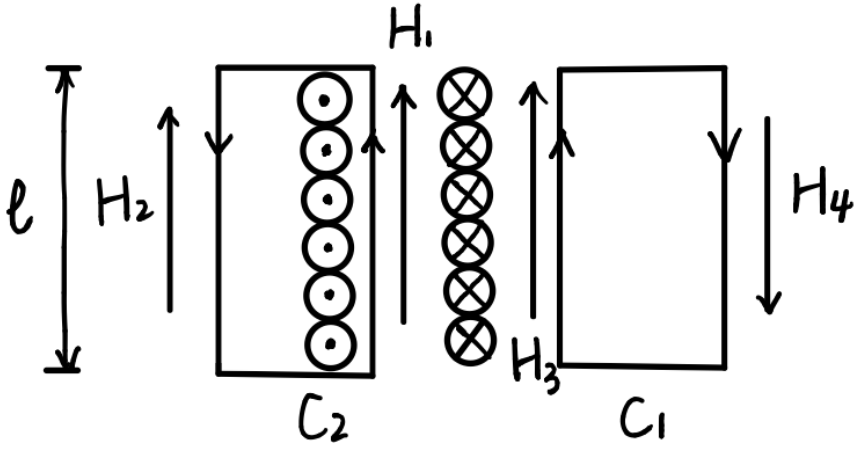
積分路
よって、
コアの外側では,磁界がゼロとなる。
(c)
(d)
(e)
従って、