東京工業大学 工学院 電気電子系 2019年8月実施 電磁気学1
留学警示(商务部公告2026年第12号)
根据中华人民共和国商务部公告2026年第12号,东京科学大学(東京科学大学/Institute of Science Tokyo)已被列入关注名单。请中国留学申请者慎重考虑相关风险,在做出留学决定前充分了解相关政策及其可能带来的影响。
Author
Zero
Description
設問 (1)~(2) を通して全ての領域で誘電率を
(1) 図
-
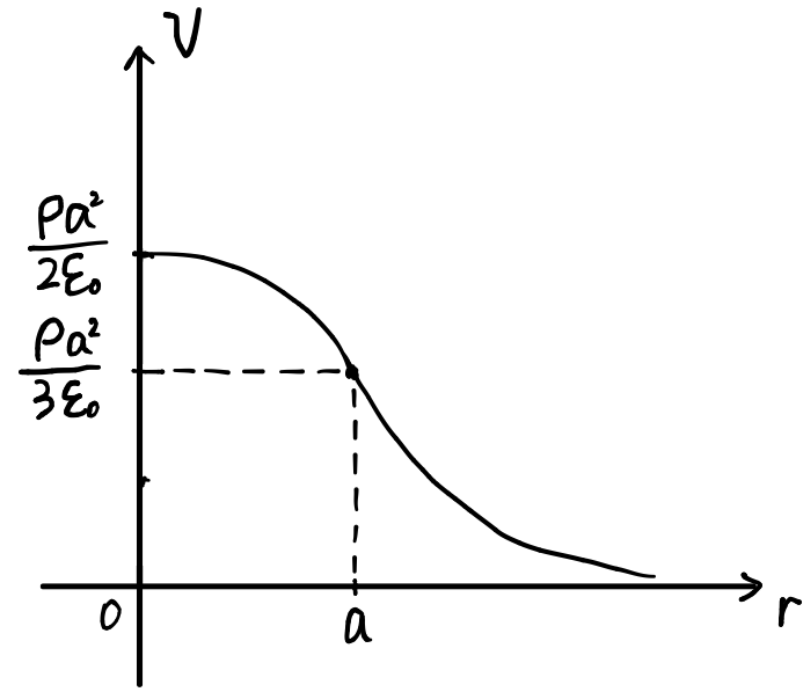
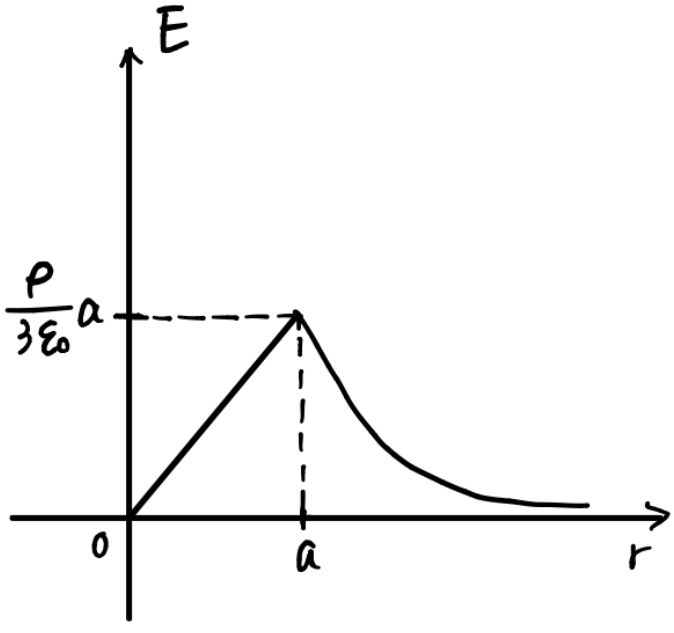
(a) 球の中心 O から距離
の点における電界の大きさ を求め, に対する変化の概略をグラフに示せ。 -
(b) 球の中心 O から距離
の点における電位 を求め, に対する変化の概略をグラフに示せ。ただし,無限遠を電位の基準 とする。 -
(c) 図
のように球の中心 O を原点として直交座標の 軸を定めたとき, の位置における 各方向の電界成分 を求めよ。 原点から点
方向の単位ベクトルが であることを利用せよ。ただし, である。

(2)
-
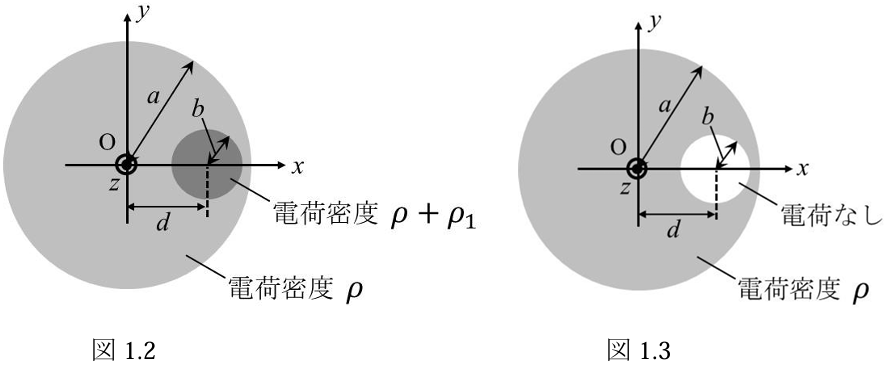
(a) 図
のように,図 の球状に分布した電荷に,位置 を中心とする半径 の球状に分布した電荷を追加した。ただし, および であり,電荷を追加した領域の単位体積当たりの電荷密度は一定値 になった。 新しく電荷を追加した領域内部での
各方向の電界成分 を求めよ。 -
(b) 図
のように,図 の球状に分布した電荷のうち,位置 を中心とする半径 の球内の電荷を取り去ると,この領域内部では電界の方向と大きさが一定となる。その方向と大きさを求めよ。ただし,(a) と同じく および とする。
Kai
(1)
(a)
(b)